Oscillatore armonico - Harmonic oscillator

Parte di una serie su
Meccanica classica
${\displaystyle {\textbf {F}}={\frac {d}{dt}}(m{\textbf {v}})}$ Seconda legge del moto
Storia Sequenza temporale libri di testo
Rami
Fondamenti
formulazioni
Argomenti principali
Rotazione
Scienziati
portale di fisica  Categoria
v T e

In meccanica classica , un oscillatore armonico è un sistema che, spostato dalla sua posizione di equilibrio , subisce una forza di richiamo F proporzionale allo spostamento x :

${\displaystyle {\vec {F}}=-k{\vec {x}},}$

dove k è una costante positiva .

Se F è l'unica forza agente sul sistema, il sistema è detto oscillatore armonico semplice , e subisce un moto armonico semplice : oscillazioni sinusoidali attorno al punto di equilibrio, di ampiezza e frequenza costanti (che non dipendono dall'ampiezza ).

Se è presente anche una forza di attrito ( smorzamento ) proporzionale alla velocità , l'oscillatore armonico viene descritto come oscillatore smorzato . A seconda del coefficiente di attrito, il sistema può:

• Oscilla con una frequenza inferiore rispetto al caso non smorzato e un'ampiezza decrescente con il tempo ( oscillatore sottosmorzato ).
• Decadimento alla posizione di equilibrio, senza oscillazioni ( oscillatore sovrasmorzato ).

La soluzione di confine tra un oscillatore sottosmorzato e un oscillatore sovrasmorzato si verifica ad un particolare valore del coefficiente di attrito e viene chiamata smorzamento critico .

Se è presente una forza esterna dipendente dal tempo, l'oscillatore armonico è descritto come un oscillatore guidato .

Esempi meccanici includono pendoli (con piccoli angoli di spostamento ), masse collegate a molle e sistemi acustici . Altri sistemi analoghi includono oscillatori armonici elettrici come i circuiti RLC . Il modello dell'oscillatore armonico è molto importante in fisica, perché qualsiasi massa soggetta a una forza in equilibrio stabile agisce come un oscillatore armonico per piccole vibrazioni. Gli oscillatori armonici si trovano ampiamente in natura e sono sfruttati in molti dispositivi artificiali, come orologi e circuiti radio. Sono la fonte di quasi tutte le vibrazioni e le onde sinusoidali.

Oscillatore armonico semplice

Un semplice oscillatore armonico è un oscillatore che non è né pilotato né smorzato . Consiste in una massa m , che subisce un'unica forza F , che trascina la massa nella direzione del punto x  = 0 e dipende solo dalla posizione x della massa e da una costante k . L'equilibrio delle forze ( seconda legge di Newton ) per il sistema è

${\displaystyle F=ma=m{\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}=m{\ddot {x}}=-kx.}$

Risolvendo questa equazione differenziale , troviamo che il moto è descritto dalla funzione

${\displaystyle x(t)=A\cos(\omega t+\varphi),}$

dove

${\displaystyle \omega ={\sqrt {\frac {k}{m}}}.}$

Il moto è periodico , ripetendosi in modo sinusoidale con ampiezza A costante . Oltre alla sua ampiezza, il moto di un oscillatore armonico semplice è caratterizzato dal suo periodo , il tempo per una singola oscillazione o la sua frequenza , il numero di cicli per unità di tempo. La posizione in un dato tempo t dipende anche dalla fase φ , che determina il punto di partenza sull'onda sinusoidale. Il periodo e la frequenza sono determinati dalla dimensione della massa m e dalla costante di forza k , mentre l'ampiezza e la fase sono determinate dalla posizione e dalla velocità di partenza . ${\displaystyle T=2\pi /\omega}$${\displaystyle f=1/T}$

La velocità e l' accelerazione di un oscillatore armonico semplice oscillano con la stessa frequenza della posizione, ma con fasi sfasate. La velocità è massima per spostamento nullo, mentre l'accelerazione è nella direzione opposta allo spostamento.

L'energia potenziale immagazzinata in un oscillatore armonico semplice nella posizione x è

${\displaystyle U={\frac {1}{2}}kx^{2}.}$

Oscillatore armonico smorzato

Negli oscillatori reali, l'attrito, o smorzamento, rallenta il movimento del sistema. A causa della forza di attrito, la velocità diminuisce in proporzione alla forza di attrito agente. Mentre in un semplice oscillatore armonico non pilotato l'unica forza che agisce sulla massa è la forza di richiamo, in un oscillatore armonico smorzato vi è inoltre una forza di attrito che è sempre in una direzione contraria al moto. In molti sistemi vibranti la forza di attrito F _f può essere modellata come proporzionale alla velocità v dell'oggetto: F _f = − cv , dove c è chiamato coefficiente di smorzamento viscoso .

Il bilancio delle forze ( seconda legge di Newton ) per oscillatori armonici smorzati è quindi

${\displaystyle F=-kx-c{\frac {\mathrm {d} x}{\mathrm {d} t}}=m{\frac {\mathrm {d} ^{2}x}{\mathrm { d} t^{2}}},}$

che può essere riscritto nella forma

${\displaystyle {\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}+2\zeta \omega _{0}{\frac {\mathrm {d} x}{\mathrm {d} t}}+\omega _{0}^{2}x=0,}$

dove

${\displaystyle \omega _{0}={\sqrt {\frac {k}{m}}}}$è chiamata la " frequenza angolare non smorzata dell'oscillatore",

${\displaystyle \zeta ={\frac {c}{2{\sqrt {mk}}}}}$ si chiama "rapporto di smorzamento".

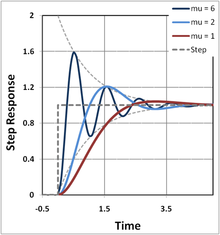
Il valore del rapporto di smorzamento ζ determina in modo critico il comportamento del sistema. Un oscillatore armonico smorzato può essere:

• Sovrasmorzato ( ζ > 1): Il sistema ritorna ( decade esponenzialmente ) allo stato stazionario senza oscillare. Valori maggiori del rapporto di smorzamento ζ ritorno all'equilibrio più lentamente.
• Smorzamento critico ( ζ = 1): il sistema ritorna allo stato stazionario il più rapidamente possibile senza oscillare (sebbene si possa verificare un superamento se la velocità iniziale è diversa da zero). Questo è spesso desiderato per lo smorzamento di sistemi come le porte.
• Sottosmorzato ( ζ < 1): Il sistema oscilla (con una frequenza leggermente diversa rispetto al caso non smorzato) con l'ampiezza che diminuisce gradualmente fino a zero. La frequenza angolare dell'oscillatore armonico sottosmorzato è dato dalla il decadimento esponenziale dell'oscillatore armonico sottosmorzato è dato da${\displaystyle \omega _{1}=\omega _{0}{\sqrt {1-\zeta ^{2}}},}$${\displaystyle \lambda =\omega _{0}\zeta.}$

Il fattore Q di un oscillatore smorzato è definito come

${\displaystyle Q=2\pi \times {\frac {\text{energia immagazzinata}}{\text{energia persa per ciclo}}}.}$

Q è correlato al rapporto di smorzamento dall'equazione${\displaystyle Q={\frac {1}{2\zeta }}.}$

Oscillatori armonici pilotati

Gli oscillatori armonici pilotati sono oscillatori smorzati ulteriormente influenzati da una forza applicata esternamente F ( t ).

La seconda legge di Newton assume la forma

${\displaystyle F(t)-kx-c{\frac {\mathrm {d} x}{\mathrm {d} t}}=m{\frac {\mathrm {d} ^{2}x}{\ mathrm {d} t^{2}}}.}$

Di solito viene riscritto nella forma

${\displaystyle {\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}+2\zeta \omega _{0}{\frac {\mathrm {d} x}{\mathrm {d} t}}+\omega _{0}^{2}x={\frac {F(t)}{m}}.}$

Questa equazione può essere risolta esattamente per qualsiasi forza motrice, usando le soluzioni z ( t ) che soddisfano l'equazione non forzata

${\displaystyle {\frac {\mathrm {d} ^{2}z}{\mathrm {d} t^{2}}}+2\zeta \omega _{0}{\frac {\mathrm {d} z}{\mathrm {d} t}}+\omega _{0}^{2}z=0,}$

e che possono essere espresse come oscillazioni sinusoidali smorzate:

${\displaystyle z(t)=A\mathrm {e} ^{-\zeta \omega _{0}t}\sin \left({\sqrt {1-\zeta ^{2}}}\omega _{ 0}t+\varphi \right),}$

nel caso in cui ζ  ≤ 1. L'ampiezza A e la fase φ determinano il comportamento necessario per soddisfare le condizioni iniziali.

Ingresso passo

Nel caso ζ  < 1 e un ingresso a gradino unitario con  x (0) = 0:

${\displaystyle {\frac {F(t)}{m}}={\begin{casi}\omega _{0}^{2}&t\geq 0\\0&t<0\end{casi}}}$

la soluzione è

${\displaystyle x(t)=1-\mathrm {e} ^{-\zeta \omega _{0}t}{\frac {\sin \left({\sqrt {1-\zeta ^{2}} }\omega _{0}t+\varphi \right)}{\sin(\varphi )}},}$

con la fase Phi dato da

${\displaystyle \cos \varphi =\zeta.}$

Il tempo necessario a un oscillatore per adattarsi alle mutate condizioni esterne è dell'ordine τ  = 1/( ζω ₀ ). In fisica, l'adattamento è chiamato il relax , e τ è chiamato il tempo di rilassamento.

In ingegneria elettrica, un multiplo di τ è chiamato il tempo di assestamento , cioè il tempo necessario a garantire il segnale si trova entro una partenza fisso dal valore finale, tipicamente entro 10%. Il termine overshoot si riferisce alla misura in cui la risposta massima supera il valore finale e undershoot si riferisce alla misura in cui la risposta scende al di sotto del valore finale per periodi successivi al massimo di risposta.

Forza motrice sinusoidale

Nel caso di una forza motrice sinusoidale:

${\displaystyle {\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}+2\zeta \omega _{0}{\frac {\mathrm {d} x}{\mathrm {d} t}}+\omega _{0}^{2}x={\frac {1}{m}}F_{0}\sin(\omega t),}$

dove è l'ampiezza di azionamento ed è la frequenza di azionamento per un meccanismo di azionamento sinusoidale. Questo tipo di sistema appare in AC -Driven circuiti RLC ( resistore - induttore - condensatore ) e sistemi di molle azionati aventi resistenza meccanica interna o esterna resistenza dell'aria . ${\displaystyle F_{0}}$${\displaystyle\omega}$

La soluzione generale è una somma di una soluzione transitoria che dipende dalle condizioni iniziali e uno stato stazionario che è indipendente dalle condizioni iniziali e dipende solo dall'ampiezza di pilotaggio , dalla frequenza di pilotaggio , dalla frequenza angolare non smorzata e dal rapporto di smorzamento . ${\displaystyle F_{0}}$${\displaystyle\omega}$${\displaystyle \omega _{0}}$${\displaystyle\zeta}$

La soluzione in regime stazionario è proporzionale alla forza motrice con un cambiamento di fase indotto : ${\displaystyle \varphi}$

${\displaystyle x(t)={\frac {F_{0}}{mZ_{m}\omega }}\sin(\omega t+\varphi),}$

dove

${\displaystyle Z_{m}={\sqrt {\left(2\omega _{0}\zeta \right)^{2}+{\frac {1}{\omega ^{2}}}(\omega _{0}^{2}-\omega ^{2})^{2}}}}$

è il valore assoluto dell'impedenza o della funzione di risposta lineare , e

${\displaystyle \varphi =\arctan \left({\frac {2\omega \omega _{0}\zeta }{\omega ^{2}-\omega _{0}^{2}}}\right) +n\pi}$

è la fase dell'oscillazione relativa alla forza motrice. Il valore di fase è generalmente considerato compreso tra -180° e 0 (cioè rappresenta un ritardo di fase, sia per i valori positivi che per quelli negativi dell'argomento arctan).

Per una particolare frequenza di guida chiamata risonanza , o frequenza di risonanza , l'ampiezza (per un dato ) è massima. Questo effetto di risonanza si verifica solo quando , cioè per sistemi notevolmente smorzati. Per sistemi fortemente smorzati il ​​valore dell'ampiezza può diventare piuttosto grande vicino alla frequenza di risonanza. ${\displaystyle \omega _{r}=\omega _{0}{\sqrt {1-2\zeta ^{2}}}}$${\displaystyle F_{0}}$${\displaystyle \zeta <1/{\sqrt {2}}}$

Le soluzioni transitorie sono le stesse dell'oscillatore armonico smorzato non forzato ( ) e rappresentano la risposta del sistema ad altri eventi che si sono verificati in precedenza. Le soluzioni transitorie in genere si estinguono abbastanza rapidamente da poter essere ignorate. ${\displaystyle F_{0}=0}$

Oscillatori parametrici

Un oscillatore parametrico è un oscillatore armonico guidato in cui l'energia di azionamento viene fornita variando i parametri dell'oscillatore, come lo smorzamento o la forza di ripristino. Un esempio familiare di oscillazione parametrica è il "pompaggio" su un'altalena da parco giochi . Una persona su un'altalena in movimento può aumentare l'ampiezza delle oscillazioni dell'altalena senza che venga applicata alcuna forza motrice esterna (spinte), modificando il momento di inerzia dell'altalena oscillando avanti e indietro ("pompaggio") o alternativamente in piedi e accovacciati, al ritmo delle oscillazioni dello swing. La variazione dei parametri guida il sistema. Esempi di parametri che possono essere variati sono la frequenza di risonanza e lo smorzamento . ${\displaystyle\omega}$${\displaystyle \beta}$

Gli oscillatori parametrici sono utilizzati in molte applicazioni. Il classico oscillatore parametrico varactor oscilla quando la capacità del diodo viene variata periodicamente. Il circuito che varia la capacità del diodo è chiamato "pompa" o "driver". Nell'elettronica a microonde, gli oscillatori parametrici basati su guida d'onda / YAG funzionano allo stesso modo. Il progettista varia periodicamente un parametro per indurre oscillazioni.

Gli oscillatori parametrici sono stati sviluppati come amplificatori a basso rumore, specialmente nella gamma di frequenze radio e microonde. Il rumore termico è minimo, poiché viene variata una reattanza (non una resistenza). Un altro uso comune è la conversione di frequenza, ad esempio la conversione da frequenze audio a frequenze radio. Ad esempio, l' oscillatore parametrico ottico converte un'onda laser in ingresso in due onde in uscita di frequenza inferiore ( ). ${\displaystyle \omega _{s},\omega _{i}}$

La risonanza parametrica si verifica in un sistema meccanico quando un sistema è eccitato parametricamente e oscilla a una delle sue frequenze di risonanza. L'eccitazione parametrica differisce dalla forzatura, poiché l'azione appare come una modifica variabile nel tempo su un parametro di sistema. Questo effetto è diverso dalla risonanza regolare perché mostra il fenomeno dell'instabilità .

Equazione dell'oscillatore universale

L'equazione

${\displaystyle {\frac {\mathrm {d} ^{2}q}{\mathrm {d} \tau ^{2}}}+2\zeta {\frac {\mathrm {d} q}{\mathrm {d} \tau }}+q=0}$

è nota come equazione dell'oscillatore universale , poiché tutti i sistemi oscillatori lineari del secondo ordine possono essere ridotti a questa forma. Questo viene fatto attraverso la non dimensionalizzazione .

Se la funzione di forzatura è f ( t ) = cos( ωt ) = cos( ωt _c τ ) = cos( ωτ ), dove ω  =  ωt _c , l'equazione diventa

${\displaystyle {\frac {\mathrm {d} ^{2}q}{\mathrm {d} \tau ^{2}}}+2\zeta {\frac {\mathrm {d} q}{\mathrm {d} \tau }}+q=\cos(\omega \tau ).}$

La soluzione a questa equazione differenziale contiene due parti: il "transitorio" e lo "stato stazionario".

Soluzione transitoria

La soluzione basata sulla risoluzione dell'equazione differenziale ordinaria è per le costanti arbitrarie c ₁ e c ₂

${\displaystyle q_{t}(\tau)={\begin{casi}\mathrm {e} ^{-\zeta \tau}\left(c_{1}\mathrm {e} ^{\tau {\sqrt {\zeta ^{2}-1}}}+c_{2}\mathrm {e} ^{-\tau {\sqrt {\zeta ^{2}-1}}}\right)&\zeta >1 {\text{ (sovrasmorzamento)}}\\\mathrm {e} ^{-\zeta \tau }(c_{1}+c_{2}\tau )=\mathrm {e} ^{-\tau }( c_{1}+c_{2}\tau )&\zeta =1{\text{ (smorzamento critico)}}\\\mathrm {e} ^{-\zeta \tau }\left[c_{1}\ cos \left({\sqrt {1-\zeta ^{2}}}\tau \right)+c_{2}\sin \left({\sqrt {1-\zeta ^{2}}}\tau \ destra)\destra]&\zeta <1{\text{ (smorzamento)}}\end{casi}}}$

La soluzione transitoria è indipendente dalla funzione di forzatura.

Soluzione allo stato stazionario

Applicare il " metodo delle variabili complesse " risolvendo l'equazione ausiliaria sottostante e quindi trovando la parte reale della sua soluzione:

${\displaystyle {\frac {\mathrm {d} ^{2}q}{\mathrm {d} \tau ^{2}}}+2\zeta {\frac {\mathrm {d} q}{\mathrm {d} \tau }}+q=\cos(\omega \tau )+\mathrm {i} \sin(\omega \tau )=\mathrm {e} ^{\mathrm {i} \omega \tau} .}$

Supponiamo che la soluzione sia della forma

${\displaystyle q_{s}(\tau)=A\mathrm {e} ^{\mathrm {i} (\omega \tau +\varphi)}.}$

Le sue derivate dallo zero al secondo ordine sono

${\displaystyle q_{s}=A\mathrm {e} ^{\mathrm {i} (\omega \tau +\varphi)},\quad {\frac {\mathrm {d} q_{s}}{\ mathrm {d} \tau}}=\mathrm {i} \omega A\mathrm {e} ^{\mathrm {i} (\omega \tau +\varphi)},\quad {\frac {\mathrm {d } ^{2}q_{s}}{\mathrm {d} \tau ^{2}}}=-\omega ^{2}A\mathrm {e} ^{\mathrm {i} (\omega \tau +\varphi )}.}$

Sostituendo queste quantità nell'equazione differenziale si ottiene

${\displaystyle -\omega ^{2}A\mathrm {e} ^{\mathrm {i} (\omega \tau +\varphi)}+2\zeta \mathrm {i} \omega A\mathrm {e} ^{\mathrm {i} (\omega \tau +\varphi )}+A\mathrm {e} ^{\mathrm {i} (\omega \tau +\varphi )}=(-\omega ^{2} A + 2 \ zeta \ mathrm {i} \ omega A + A) \ mathrm {e} ^ {\ mathrm {i} (\ omega \ tau + \ varphi )} = \ mathrm {e} ^ {\ mathrm {i } \omega \tau }.}$

Dividendo per il termine esponenziale a sinistra si ottiene

${\displaystyle -\omega ^{2}A+2\zeta \mathrm {i} \omega A+A=\mathrm {e} ^{-\mathrm {i} \varphi }=\cos \varphi -\mathrm {i} \sin \varphi .}$

Uguagliando le parti reale e immaginaria si ottengono due equazioni indipendenti

${\displaystyle A(1-\omega ^{2})=\cos \varphi ,\quad 2\zeta \omega A=-\sin \varphi .}$

Ampiezza parte

Elevando al quadrato entrambe le equazioni e sommandole si ottiene

${\displaystyle \left.{\begin{aligned}A^{2}(1-\omega ^{2})^{2}&=\cos ^{2}\varphi \\(2\zeta \omega A )^{2}&=\sin ^{2}\varphi \end{aligned}}\right\}\Rightarrow A^{2}[(1-\omega ^{2})^{2}+(2 \zeta \omega )^{2}]=1.}$

Perciò,

${\displaystyle A=A(\zeta,\omega)=\operatorname {segno} \left({\frac {-\sin \varphi}}{2\zeta \omega }}\right){\frac {1}{ \sqrt {(1-\omega ^{2})^{2}+(2\zeta \omega )^{2}}}}.}$

Confronta questo risultato con la sezione teorica sulla risonanza , nonché la "parte di magnitudo" del circuito RLC . Questa funzione di ampiezza è particolarmente importante nell'analisi e nella comprensione della risposta in frequenza dei sistemi del secondo ordine.

Parte di fase

Per risolvere per φ , dividi entrambe le equazioni per ottenere

${\displaystyle \tan \varphi =-{\frac {2\zeta \omega {1-\omega ^{2}}}={\frac {2\zeta \omega }{\omega ^{2}-1 }}\Rightarrow \varphi \equiv \varphi (\zeta ,\omega )=\arctan \left({\frac {2\zeta \omega }{\omega ^{2}-1}}\right)+n\ pi.}$

Questa funzione di fase è particolarmente importante nell'analisi e nella comprensione della risposta in frequenza dei sistemi del secondo ordine.

Soluzione completa

Combinando le porzioni di ampiezza e fase si ottiene la soluzione allo stato stazionario

${\displaystyle q_{s}(\tau)=A(\zeta,\omega)\cos(\omega \tau +\varphi (\zeta,\omega))=A\cos(\omega \tau +\varphi ).}$

La soluzione dell'equazione originale dell'oscillatore universale è una sovrapposizione (somma) delle soluzioni transitorie e stazionarie:

${\displaystyle q(\tau)=q_{t}(\tau)+q_{s}(\tau).}$

Per una descrizione più completa di come risolvere l'equazione di cui sopra, vedere ODE lineari con coefficienti costanti .

Sistemi equivalenti

Gli oscillatori armonici che si verificano in un certo numero di aree dell'ingegneria sono equivalenti nel senso che i loro modelli matematici sono identici (vedi l'equazione dell'oscillatore universale sopra). Di seguito è riportata una tabella che mostra quantità analoghe in quattro sistemi di oscillatori armonici in meccanica ed elettronica. Se a parametri analoghi sulla stessa riga della tabella vengono dati valori numericamente uguali, il comportamento degli oscillatori – forma d'onda di uscita, frequenza di risonanza, fattore di smorzamento, ecc. – è lo stesso.

Meccanica traslazionale	Meccanico rotazionale	Circuito serie RLC	Circuito RLC parallelo
Posizione ${\displaystyle x}$	Angolo ${\displaystyle \theta}$	Carica ${\displaystyle q}$	Collegamento del flusso ${\displaystyle \varphi}$
Velocità ${\displaystyle {\frac {\mathrm {d} x}{\mathrm {d} t}}}$	Velocità angolare ${\ Displaystyle {\ frac {\ mathrm {d} \ theta} {\ mathrm {d} t}}}$	Attuale ${\displaystyle {\frac {\mathrm {d} q}{\mathrm {d} t}}}$	Voltaggio ${\displaystyle {\frac {\mathrm {d} \varphi}}\mathrm {d} t}}}$
Messa ${\displaystyle m}$	Momento d'inerzia ${\displaystyle io}$	Induttanza ${\displaystyle L}$	Capacità ${\displaystyle C}$
Quantità di moto ${\displaystyle p}$	Momento angolare ${\displaystyle L}$	Collegamento del flusso ${\displaystyle \varphi}$	Carica ${\displaystyle q}$
Costante di primavera ${\displaystyle k}$	Costante di torsione ${\displaystyle\mu}$	elastanza ${\displaystyle 1/C}$	Riluttanza magnetica ${\displaystyle 1/L}$
smorzamento ${\displaystyle c}$	Attrito rotazionale ${\displaystyle \Gamma}$	Resistenza ${\displaystyle R}$	Conduttanza ${\displaystyle G=1/R}$
Forza motrice ${\displaystyle F(t)}$	azionamento coppia ${\displaystyle \tau(t)}$	Voltaggio ${\displaystyle e}$	Attuale ${\displaystyle i}$
Frequenza di risonanza non smorzata : ${\displaystyle f_{n}}$
${\displaystyle {\frac {1}{2\pi }}{\sqrt {\frac {k}{m}}}}$	${\displaystyle {\frac {1}{2\pi }}{\sqrt {\frac {\mu }{I}}}}$	${\displaystyle {\frac {1}{2\pi }}{\sqrt {\frac {1}{LC}}}}$	${\displaystyle {\frac {1}{2\pi }}{\sqrt {\frac {1}{LC}}}}$
Rapporto di smorzamento : ${\displaystyle\zeta}$
${\displaystyle {\frac {c}{2}}{\sqrt {\frac {1}{km}}}}$	${\displaystyle {\frac {\Gamma }{2}}{\sqrt {\frac {1}{I\mu }}}}$	${\displaystyle {\frac {R}{2}}{\sqrt {\frac {C}{L}}}}$	${\displaystyle {\frac {G}{2}}{\sqrt {\frac {L}{C}}}}$
Equazione differenziale:
${\displaystyle m{\ddot {x}}+c{\dot {x}}+kx=F}$	${\displaystyle I{\ddot {\theta}}+\Gamma {\dot {\theta}}+\mu \theta =\tau}$	${\displaystyle L{\ddot {q}}+R{\dot {q}}+q/C=e}$	${\displaystyle C{\ddot {\varphi}}+G{\dot {\varphi}}+\varphi /L=i}$

Applicazione a una forza conservativa

Il problema dell'oscillatore armonico semplice si presenta frequentemente in fisica, perché una massa in equilibrio sotto l'influenza di una qualsiasi forza conservativa , nel limite dei piccoli moti, si comporta come un oscillatore armonico semplice.

Una forza conservativa è quella associata a un'energia potenziale . La funzione di energia potenziale di un oscillatore armonico è

${\displaystyle V(x)={\frac {1}{2}}kx^{2}.}$

Data una funzione di energia potenziale arbitraria , si può fare uno sviluppo di Taylor in termini di circa un minimo di energia ( ) per modellare il comportamento di piccole perturbazioni dall'equilibrio. ${\displaystyle V(x)}$${\displaystyle x}$${\displaystyle x=x_{0}}$

${\displaystyle V(x)=V(x_{0})+V'(x_{0})\cdot (x-x_{0})+{\frac {1}{2}}V^{(2 )}(x_{0})\cdot (x-x_{0})^{2}+O(x-x_{0})^{3}.}$

Poiché è un minimo, la prima derivata valutata a deve essere zero, quindi il termine lineare viene eliminato: ${\displaystyle V(x_{0})}$${\displaystyle x_{0}}$

${\displaystyle V(x)=V(x_{0})+{\frac {1}{2}}V^{(2)}(x_{0})\cdot (x-x_{0})^ {2}+O(x-x_{0})^{3}.}$

Il termine costante V ( x ₀ ) è arbitrario e quindi può essere eliminato, e una trasformazione di coordinate consente di recuperare la forma dell'oscillatore armonico semplice:

${\displaystyle V(x)\circa {\frac {1}{2}}V^{(2)}(0)\cdot x^{2}={\frac {1}{2}}kx^{ 2}.}$

Quindi, data una funzione arbitraria di energia potenziale con una seconda derivata non nulla, si può usare la soluzione dell'oscillatore armonico semplice per fornire una soluzione approssimata per piccole perturbazioni attorno al punto di equilibrio. ${\displaystyle V(x)}$

Esempi

Pendolo semplice

Assumendo nessun smorzamento, l'equazione differenziale che governa un pendolo semplice di lunghezza , dove è l' accelerazione locale di gravità , è ${\displaystyle l}$${\displaystyle g}$

${\displaystyle {\frac {d^{2}\theta }{dt^{2}}}+{\frac {g}{l}}\sin \theta =0.}$

Se lo spostamento massimo del pendolo è piccolo, possiamo usare l'approssimazione e considerare invece l'equazione ${\displaystyle \sin \theta \about \theta }$

${\displaystyle {\frac {d^{2}\theta }{dt^{2}}}+{\frac {g}{l}}\theta =0.}$

La soluzione generale di questa equazione differenziale è

${\displaystyle \theta (t)=A\cos \left({\sqrt {\frac {g}{l}}}t+\varphi \right),}$

dove e sono costanti che dipendono dalle condizioni iniziali. Usando come condizioni iniziali e , la soluzione è data da ${\displaystyle A}$${\displaystyle \varphi}$${\displaystyle \theta (0)=\theta _{0}}$${\displaystyle {\dot {\theta}}(0)=0}$

${\displaystyle \theta (t)=\theta _{0}\cos \left({\sqrt {\frac {g}{l}}}t\right),}$

dove è l'angolo più grande raggiunto dal pendolo (cioè è l'ampiezza del pendolo). Il periodo , il tempo per un'oscillazione completa, è dato dall'espressione ${\displaystyle \theta _{0}}$${\displaystyle \theta _{0}}$

${\ Displaystyle \ tau = 2 \ pi {\ sqrt {\ frac {l} {g}}} = {\ frac {2 \ pi {\ omega}},}$

che è una buona approssimazione del periodo effettivo quando è piccolo. Si noti che in questa approssimazione il periodo è indipendente dall'ampiezza . Nell'equazione sopra, rappresenta la frequenza angolare. ${\displaystyle \theta _{0}}$${\displaystyle \tau}$${\displaystyle \theta _{0}}$${\displaystyle\omega}$

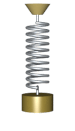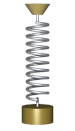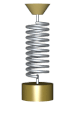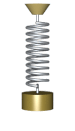
Sistema molla/massa

Quando una molla viene allungata o compressa da una massa, la molla sviluppa una forza di richiamo. La legge di Hooke fornisce il rapporto della forza esercitata dalla molla quando la molla viene compressa o allungata per una certa lunghezza:

${\displaystyle F(t)=-kx(t),}$

dove F è la forza, k è la costante elastica e x è lo spostamento della massa rispetto alla posizione di equilibrio. Il segno meno nell'equazione indica che la forza esercitata dalla molla agisce sempre in direzione opposta allo spostamento (cioè la forza agisce sempre verso la posizione zero), e quindi impedisce alla massa di volare all'infinito.

Usando il bilancio delle forze o un metodo energetico, si può facilmente dimostrare che il moto di questo sistema è dato dalla seguente equazione differenziale:

${\displaystyle F(t)=-kx(t)=m{\frac {\mathrm {d} ^{2}}{\mathrm {d} t^{2}}}x(t)=ma,}$

quest'ultima è la seconda legge del moto di Newton .

Se lo spostamento iniziale è A , e non c'è velocità iniziale, la soluzione di questa equazione è data da

${\displaystyle x(t)=A\cos \left({\sqrt {\frac {k}{m}}}t\right).}$

Data una molla ideale senza massa, è la massa all'estremità della molla. Se la molla stessa ha massa, la sua massa effettiva deve essere inclusa in . ${\displaystyle m}$${\displaystyle m}$

Variazione di energia nel sistema di smorzamento a molla

In termini di energia, tutti i sistemi hanno due tipi di energia: energia potenziale ed energia cinetica . Quando una molla viene allungata o compressa, immagazzina energia potenziale elastica, che viene poi trasferita in energia cinetica. L'energia potenziale all'interno di una molla è determinata dall'equazione${\displaystyle U=kx^{2}/2.}$

Quando la molla viene allungata o compressa, l'energia cinetica della massa viene convertita in energia potenziale della molla. Per conservazione dell'energia, assumendo che il dato sia definito nella posizione di equilibrio, quando la molla raggiunge la sua massima energia potenziale, l'energia cinetica della massa è nulla. Quando la molla viene rilasciata, cerca di tornare all'equilibrio e tutta la sua energia potenziale si converte in energia cinetica della massa.

Definizione dei termini

Simbolo	Definizione	Dimensioni	unità SI
${\displaystyle a}$	Accelerazione di massa	${\displaystyle \mathbf {LT^{-2}} }$	m/s 2
${\displaystyle A}$	Ampiezza di picco dell'oscillazione	${\displaystyle \mathbf {L}}$	m
${\displaystyle c}$	Coefficiente di smorzamento viscoso	${\displaystyle \mathbf {MT^{-1}} }$	N·s/m
${\displaystyle f}$	Frequenza	${\displaystyle \mathbf {T^{-1}} }$	Hz
${\displaystyle F}$	Forza motrice	${\displaystyle \mathbf {MLT^{-2}} }$	n
${\displaystyle g}$	Accelerazione di gravità sulla superficie terrestre	${\displaystyle \mathbf {LT^{-2}} }$	m/s 2
${\displaystyle i}$	unità immaginaria, ${\displaystyle i^{2}=-1}$	—	—
${\displaystyle k}$	Costante di primavera	${\displaystyle \mathbf {MT^{-2}} }$	N/m
${\displaystyle m, M}$	Messa	${\displaystyle \mathbf {M}}$	kg
${\displaystyle Q}$	Fattore di qualità	—	—
${\displaystyle T}$	Periodo di oscillazione	${\displaystyle \mathbf {T} }$	S
${\displaystyle}$	Tempo	${\displaystyle \mathbf {T} }$	S
${\displaystyle U}$	Energia potenziale immagazzinata nell'oscillatore	${\displaystyle \mathbf {ML^{2}T^{-2}} }$	J
${\displaystyle x}$	Posizione della massa	${\displaystyle \mathbf {L}}$	m
${\displaystyle\zeta}$	Rapporto di smorzamento	—	—
${\displaystyle \varphi}$	Sfasamento	—	rad
${\displaystyle\omega}$	Frequenza angolare	${\displaystyle \mathbf {T^{-1}} }$	rad/s
${\displaystyle \omega _{0}}$	Frequenza angolare di risonanza naturale	${\displaystyle \mathbf {T^{-1}} }$	rad/s

Guarda anche

• Oscillatore anarmonico
• Velocità critica
• Massa effettiva (sistema molla-massa)
• Modalità normale
• Oscillatore parametrico
• Fasore
• Fattore Q
• Oscillatore armonico quantistico
• Oscillatore armonico radiale
• Pendolo elastico

Appunti

Riferimenti

• Fowles, Grant R.; Cassiday, George L. (1986), Meccanica analitica (5a ed.), Fort Worth: Saunders College Publishing , ISBN 0-03-96746-5, LCCN  93085193Manutenzione CS1: errori ISBN ignorati ( link )
• Hayek, Sabih I. (15 aprile 2003). "Vibrazioni meccaniche e smorzamento". Enciclopedia della fisica applicata . WILEY-VCH Verlag GmbH & Co KGaA. doi : 10.1002/3527600434.eap231 . ISBN 9783527600434.
• Kreyszig, Erwin (1972), Advanced Engineering Mathematics (3a ed.), New York: Wiley , ISBN 0-471-50728-8
• Serway, Raymond A.; Jewett, John W. (2003). Fisica per scienziati e ingegneri . Brooks/Cole. ISBN 0-534-40842-7.
• Tipler, Paul (1998). Fisica per scienziati e ingegneri: vol. 1 (4a ed.). WH Freeman. ISBN 1-57259-492-6.
• Wylie, CR (1975). Matematica di ingegneria avanzata (4a ed.). McGraw Hill. ISBN 0-07-072180-7.

link esterno

• L'oscillatore armonico da The Feynman Lectures on Physics