Modelli in natura - Patterns in nature


I modelli in natura sono regolarità visibili della forma che si trovano nel mondo naturale . Questi modelli ricorrono in diversi contesti e talvolta possono essere modellati matematicamente . I motivi naturali includono simmetrie , alberi , spirali , meandri , onde , schiume , tassellature , crepe e strisce. I primi filosofi greci studiarono il modello, con Platone , Pitagora ed Empedocle che tentavano di spiegare l'ordine in natura. La moderna comprensione dei modelli visibili si è sviluppata gradualmente nel tempo.
Nel XIX secolo il fisico belga Joseph Plateau esaminò le pellicole di sapone , portandolo a formulare il concetto di superficie minima . Il biologo e artista tedesco Ernst Haeckel dipinse centinaia di organismi marini per enfatizzare la loro simmetria . Il biologo scozzese D'Arcy Thompson ha aperto la strada allo studio dei modelli di crescita sia nelle piante che negli animali, dimostrando che semplici equazioni potrebbero spiegare la crescita a spirale. Nel XX secolo, il matematico britannico Alan Turing predisse meccanismi di morfogenesi che danno origine a modelli di macchie e strisce. Il biologo ungherese Aristid Lindenmayer e il matematico franco-americano Benoît Mandelbrot hanno mostrato come la matematica dei frattali potrebbe creare modelli di crescita delle piante.
La matematica , la fisica e la chimica possono spiegare i modelli in natura a diversi livelli e scale. I modelli negli esseri viventi sono spiegati dai processi biologici della selezione naturale e della selezione sessuale . Gli studi sulla formazione di modelli utilizzano modelli informatici per simulare un'ampia gamma di modelli.
Storia

I primi filosofi greci hanno tentato di spiegare l'ordine nella natura , anticipando i concetti moderni. Pitagora (c. 570-c. 495 aC) ha spiegato che i modelli in natura come le armonie della musica derivano dal numero, che considerava il costituente fondamentale dell'esistenza. Empedocle (c. 494-c. 434 aC) in una certa misura anticipava la spiegazione evoluzionistica di Darwin per le strutture degli organismi. Platone (c. 427-c. 347 aC) sostenne l'esistenza di universali naturali . Egli li considerava costituiti da forme ideali ( εἶδος eidos : "forma") di cui gli oggetti fisici non sono mai altro che copie imperfette. Quindi, un fiore può essere approssimativamente circolare, ma non è mai un cerchio perfetto. Teofrasto (c. 372-c. 287 aC) ha notato che le piante "che hanno foglie piatte le hanno in una serie regolare"; Plinio il Vecchio (23-79 d.C.) notò la loro disposizione circolare modellata. Secoli dopo, Leonardo da Vinci (1452-1519) notò la disposizione a spirale dei motivi fogliari, secondo cui i tronchi degli alberi guadagnano anelli successivi man mano che invecchiano e propose una regola presumibilmente soddisfatta dalle aree trasversali dei rami degli alberi.
Nel 1202, Leonardo Fibonacci introdusse la sequenza di Fibonacci nel mondo occidentale con il suo libro Liber Abaci . Fibonacci ha presentato un esperimento mentale sulla crescita di una popolazione di conigli idealizzata . Johannes Kepler (1571-1630) indicò la presenza della sequenza di Fibonacci in natura, utilizzandola per spiegare la forma pentagonale di alcuni fiori. Nel 1658, il medico e filosofo inglese Sir Thomas Browne discusse "come Nature Geometrizeth" in The Garden of Cyrus , citando la numerologia pitagorica che coinvolge il numero 5 e la forma platonica del modello a quinconce . Il capitolo centrale del discorso presenta esempi e osservazioni del quinconce in botanica. Nel 1754, Charles Bonnet osservò che la fillotassi a spirale delle piante era spesso espressa in serie di rapporti aurei sia in senso orario che antiorario . Le osservazioni matematiche della fillotassi sono seguite rispettivamente con i lavori del 1830 e del 1830 di Karl Friedrich Schimper e del suo amico Alexander Braun ; Auguste Bravais e suo fratello Louis collegarono i rapporti di fillotassi alla sequenza di Fibonacci nel 1837, notando anche la sua comparsa nelle pigne e negli ananas . Nel suo libro del 1854, lo psicologo tedesco Adolf Zeising esplorò il rapporto aureo espresso nella disposizione delle parti delle piante, negli scheletri degli animali e nei modelli di ramificazione delle loro vene e nervi, nonché nei cristalli .

Nel XIX secolo, il fisico belga Joseph Plateau (1801-1883) formulò il problema matematico dell'esistenza di una superficie minima con un determinato confine, che ora porta il suo nome. Studiò intensamente i film di sapone, formulando le leggi di Plateau che descrivono le strutture formate dai film nelle schiume. Lord Kelvin ha identificato il problema del modo più efficiente per imballare celle di uguale volume come schiuma nel 1887; la sua soluzione utilizza un solo solido, il nido d'ape cubico bitruncato con facce leggermente curve per soddisfare le leggi di Plateau. Nessuna soluzione migliore è stata trovata fino al 1993, quando Denis Weaire e Robert Phelan hanno proposto la struttura Weaire-Phelan ; il Centro acquatico nazionale di Pechino ha adattato la struttura per il muro esterno durante le Olimpiadi estive del 2008 . Ernst Haeckel (1834-1919) dipinse bellissime illustrazioni di organismi marini, in particolare Radiolaria , sottolineando la loro simmetria per supportare le sue finte teorie dell'evoluzione darwiniane . Il fotografo americano Wilson Bentley ha scattato la prima microfotografia di un fiocco di neve nel 1885.
Nel 20 ° secolo, AH Church ha studiato i modelli di fillotassi nel suo libro del 1904. Nel 1917, D'Arcy Wentworth Thompson pubblicò On Growth and Form ; la sua descrizione della fillotassi e della sequenza di Fibonacci, le relazioni matematiche nei modelli di crescita a spirale delle piante hanno mostrato che semplici equazioni potrebbero descrivere i modelli di crescita a spirale delle corna degli animali e dei gusci di molluschi . Nel 1952, Alan Turing (1912-1954), meglio conosciuto per il suo lavoro sull'informatica e la decrittazione del codice , scrisse The Chemical Basis of Morphogenesis , un'analisi dei meccanismi che sarebbero stati necessari per creare modelli negli organismi viventi, nel processo chiamato morfogenesi . Ha predetto reazioni chimiche oscillanti , in particolare la reazione Belousov-Zhabotinsky . Questi meccanismi attivatore-inibitore possono, suggerì Turing, generare modelli (soprannominati " modelli di Turing ") di strisce e macchie negli animali e contribuire ai modelli a spirale visti nella fillotassi delle piante. Nel 1968, il biologo teorico ungherese Aristid Lindenmayer (1925-1989) sviluppò il sistema L , una grammatica formale che può essere utilizzata per modellare i modelli di crescita delle piante nello stile dei frattali . I sistemi L hanno un alfabeto di simboli che possono essere combinati utilizzando regole di produzione per costruire stringhe di simboli più grandi e un meccanismo per tradurre le stringhe generate in strutture geometriche. Nel 1975, dopo secoli di lento sviluppo della matematica dei modelli di Gottfried Leibniz , Georg Cantor , Helge von Koch , Wacław Sierpiński e altri, Benoît Mandelbrot scrisse un famoso articolo, Quanto è lunga la costa della Gran Bretagna? Autosimilarità statistica e dimensione frazionaria , cristallizzando il pensiero matematico nel concetto di frattale .
cause
Gli esseri viventi come le orchidee , i colibrì e la coda del pavone hanno disegni astratti con una bellezza di forme, motivi e colori che gli artisti faticano a eguagliare. La bellezza che le persone percepiscono in natura ha cause a diversi livelli, in particolare nella matematica che governa quali modelli possono formarsi fisicamente e tra gli esseri viventi negli effetti della selezione naturale, che governano l'evoluzione dei modelli.
La matematica cerca di scoprire e spiegare schemi astratti o regolarità di ogni tipo. I modelli visivi in natura trovano spiegazioni nella teoria del caos , nei frattali, nelle spirali logaritmiche, nella topologia e in altri modelli matematici. Ad esempio, i sistemi L formano modelli convincenti di diversi modelli di crescita degli alberi.
Le leggi della fisica applicano le astrazioni della matematica al mondo reale, spesso come se fosse perfetto . Ad esempio, un cristallo è perfetto quando non ha difetti strutturali come dislocazioni ed è completamente simmetrico. L'esatta perfezione matematica può solo approssimare oggetti reali. I modelli visibili in natura sono governati da leggi fisiche ; per esempio, i meandri possono essere spiegati usando la fluidodinamica .
In biologia , la selezione naturale può causare lo sviluppo di modelli negli esseri viventi per diversi motivi, tra cui il camuffamento , la selezione sessuale e diversi tipi di segnalazione, tra cui il mimetismo e la simbiosi di pulizia . Nelle piante, le forme, i colori e i motivi dei fiori impollinati dagli insetti come il giglio si sono evoluti per attirare insetti come le api . I modelli radiali di colori e strisce, alcuni visibili solo alla luce ultravioletta, fungono da guide per il nettare che possono essere viste a distanza.
Tipi di pattern
Simmetria
La simmetria è pervasiva negli esseri viventi. Gli animali hanno principalmente simmetria bilaterale o speculare , così come le foglie delle piante e alcuni fiori come le orchidee . Le piante hanno spesso simmetria radiale o rotazionale , così come molti fiori e alcuni gruppi di animali come gli anemoni di mare . La simmetria quintupla si trova negli echinodermi , il gruppo che comprende stelle marine , ricci di mare e gigli di mare .
Tra le cose non viventi, i fiocchi di neve hanno una simmetria sorprendente di sei volte ; la struttura di ogni fiocco costituisce una registrazione delle condizioni variabili durante la sua cristallizzazione, con quasi lo stesso modello di crescita su ciascuno dei suoi sei bracci. I cristalli in generale hanno una varietà di simmetrie e abitudini cristalline ; possono essere cubici o ottaedrici, ma i veri cristalli non possono avere una simmetria quintuplicata (a differenza dei quasicristalli ). La simmetria rotazionale si trova a diverse scale tra gli esseri non viventi, incluso il modello di schizzi a forma di corona che si forma quando una goccia cade in uno stagno, e sia la forma sferoidale che gli anelli di un pianeta come Saturno .
La simmetria ha una varietà di cause. La simmetria radiale si adatta ad organismi come gli anemoni di mare i cui adulti non si muovono: cibo e minacce possono arrivare da qualsiasi direzione. Ma gli animali che si muovono in una direzione hanno necessariamente i lati superiore e inferiore, le estremità della testa e della coda, e quindi una sinistra e una destra. La testa si specializza con la bocca e gli organi di senso ( cefalizzazione ) e il corpo diventa simmetrico bilateralmente (sebbene gli organi interni non debbano esserlo). Più sconcertante è la ragione della quintupla (pentaradiata) simmetria degli echinodermi. I primi echinodermi erano bilateralmente simmetrici, come lo sono ancora le loro larve. Sumrall e Wray sostengono che la perdita della vecchia simmetria ha avuto cause sia evolutive che ecologiche.
Gli animali mostrano spesso una simmetria speculare o bilaterale , come questa tigre .
Gli echinodermi come questa stella marina hanno una simmetria di cinque volte .
La simmetria di cinque volte può essere vista in molti fiori e in alcuni frutti come questo nespolo .
I fiocchi di neve hanno una simmetria di sei volte .
Fluorite che mostra un abito cristallino cubico .
Gli schizzi d' acqua si avvicinano alla simmetria radiale .
Granato che mostra un abito di cristallo dodecaedrico rombico.
Volvox ha simmetria sferica.
Alberi, frattali
Il modello di ramificazione degli alberi è stato descritto nel Rinascimento italiano da Leonardo da Vinci . In Trattato sulla pittura affermava che:
Tutti i rami di un albero in ogni fase della sua altezza quando messi insieme sono uguali in spessore al tronco [sotto di loro].
Una versione più generale afferma che quando un ramo padre si divide in due o più rami figlio, le aree della superficie dei rami figlio si sommano a quella del ramo padre. Una formulazione equivalente è che se un ramo genitore si divide in due rami figli, allora i diametri della sezione trasversale del genitore e dei due rami figli formano un triangolo rettangolo . Una spiegazione è che ciò consente agli alberi di resistere meglio ai venti forti. Le simulazioni di modelli biomeccanici concordano con la regola.
I frattali sono infinitamente auto-similari , costrutti matematici iterati aventi dimensione frattale . L' iterazione infinita non è possibile in natura, quindi tutti i modelli "frattali" sono solo approssimativi. Ad esempio, le foglie di felci e ombrellifere (Apiaceae) sono solo auto-simili (pennate) a 2, 3 o 4 livelli. Modelli di crescita simili a felci si verificano nelle piante e negli animali tra cui briozoi , coralli , idrozoi come la felce aerea , Sertularia argentea e negli esseri non viventi, in particolare scariche elettriche . I frattali del sistema Lindenmayer possono modellare diversi modelli di crescita degli alberi variando un piccolo numero di parametri tra cui l'angolo di ramificazione, la distanza tra i nodi o i punti di diramazione ( lunghezza degli internodi ) e il numero di rami per punto di diramazione.
I modelli frattali si verificano ampiamente in natura, in fenomeni diversi come nuvole, reti fluviali , linee di faglia geologiche , montagne , coste , colorazione animale , fiocchi di neve , cristalli , ramificazione dei vasi sanguigni , citoscheletro di actina e onde oceaniche .
I modelli di crescita di alcuni alberi assomigliano a questi frattali del sistema Lindenmayer .
Branching modello di un baobab albero
La foglia di prezzemolo di vacca, Anthriscus sylvestris , è a 2 o 3 pennate , non infinita
Spirali frattali : broccolo romanesco che mostra una forma autosimilare
Alberi: Figura di Lichtenberg : rottura dielettrica ad alta tensione in un blocco di polimero acrilico
Alberi: cristalli di rame dendritico (al microscopio)
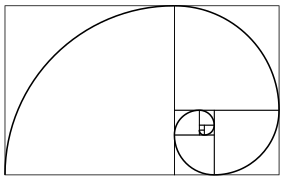
spirali
Le spirali sono comuni nelle piante e in alcuni animali, in particolare nei molluschi . Ad esempio, nel nautilus , un mollusco cefalopode, ogni camera della sua conchiglia è una copia approssimativa della successiva, ridimensionata di un fattore costante e disposta a spirale logaritmica . Data una moderna comprensione dei frattali, una spirale di crescita può essere vista come un caso speciale di autosomiglianza.
Le spirali delle piante possono essere viste nella fillotassi , la disposizione delle foglie su uno stelo, e nella disposizione ( parastichia ) di altre parti come nei capolini compositi e nei capolini dei semi come il girasole o nelle strutture dei frutti come l' ananas e il frutto del serpente , così come nello schema delle squame nelle pigne , dove più spirali corrono sia in senso orario che antiorario. Queste disposizioni hanno spiegazioni a diversi livelli – matematica, fisica, chimica, biologia – ciascuna corretta individualmente, ma tutte necessarie insieme. Le spirali di fillotassi possono essere generate matematicamente dai rapporti di Fibonacci : la sequenza di Fibonacci esegue 1, 1, 2, 3, 5, 8, 13... (ogni numero successivo è la somma dei due precedenti). Ad esempio, quando le foglie si alternano su uno stelo, una rotazione della spirale tocca due foglie, quindi il motivo o il rapporto è 1/2. In nocciola il rapporto è 1/3; in albicocca è 2/5; in pera è 3/8; in mandorla è 5/13. Nella fillotassi del disco come nel girasole e nella margherita , i fiori sono disposti a spirale di Fermat con numerazione di Fibonacci, almeno quando il capolino è maturo quindi tutti gli elementi hanno la stessa dimensione. I rapporti di Fibonacci approssimano l' angolo aureo , 137,508°, che governa la curvatura della spirale di Fermat.
Dal punto di vista della fisica, le spirali sono configurazioni a energia più bassa che emergono spontaneamente attraverso processi di auto-organizzazione in sistemi dinamici . Dal punto di vista della chimica, una spirale può essere generata da un processo di reazione-diffusione, che coinvolge sia l'attivazione che l'inibizione. La fillotassi è controllata da proteine che manipolano la concentrazione dell'ormone vegetale auxina , che attiva la crescita del meristema , insieme ad altri meccanismi per controllare l'angolo relativo delle gemme attorno allo stelo. Da un punto di vista biologico, disporre le foglie il più distanti possibile in un dato spazio è favorito dalla selezione naturale in quanto massimizza l'accesso alle risorse, in particolare alla luce solare per la fotosintesi .
Spirale di Fibonacci
Pecora dalle grandi corna , Ovis canadensis
Spirali: fillotassi di aloe a spirale, Aloe polyphylla
Spirale di crescita logaritmica della conchiglia di Nautilus
Spirale di Fermat : capolino di girasole , Helianthus annuus
Molteplici spirali di Fibonacci: cavolo rosso in sezione
Conchiglia a spirale di Trochoidea liebetruti
Goccioline d'acqua volano da una palla bagnata che gira in spirali equiangolari
Caos, flusso, meandri
In matematica, un sistema dinamico è caotico se è (altamente) sensibile alle condizioni iniziali (il cosiddetto " effetto farfalla "), che richiede proprietà matematiche di mescolamento topologico e orbite periodiche dense .
Accanto ai frattali, la teoria del caos si classifica come un'influenza essenzialmente universale sui modelli in natura. Esiste una relazione tra caos e frattali: gli strani attrattori nei sistemi caotici hanno una dimensione frattale . Alcuni automi cellulari , semplici insiemi di regole matematiche che generano schemi, hanno un comportamento caotico, in particolare la Regola 30 di Stephen Wolfram .
Le strade a vortice sono schemi a zigzag di vortici vorticosi creati dalla separazione instabile del flusso di un fluido , molto spesso aria o acqua, su oggetti che ostruiscono. Il flusso regolare ( laminare ) inizia a rompersi quando le dimensioni dell'ostruzione o la velocità del flusso diventano sufficientemente grandi rispetto alla viscosità del fluido.
I meandri sono curve sinuose in fiumi o altri canali, che si formano quando un fluido, il più delle volte acqua, scorre attorno alle curve. Non appena il percorso è leggermente curvo, le dimensioni e la curvatura di ciascun anello aumentano poiché il flusso elicoidale trascina materiale come sabbia e ghiaia attraverso il fiume all'interno dell'ansa . L'esterno dell'anello viene lasciato pulito e non protetto, quindi l' erosione accelera, aumentando ulteriormente i meandri in un potente anello di feedback positivo .
Caos: guscio di mollusco gasteropode il panno del cono d'oro, tessuto Conus , assomiglia all'automa cellulare Regola 30
Flow: vortice di nuvole alle Isole Juan Fernandez
Meandri: drammatiche cicatrici meandro e laghetti nell'ampia pianura alluvionale del Rio Negro , visto dallo spazio
Meandri: sentiero sinuoso del Rio Cauto , Cuba
Meandri: corallo cervello simmetrico , Diploria strigosa
Onde, dune
Le onde sono disturbi che trasportano energia mentre si muovono. Le onde meccaniche si propagano attraverso un mezzo – aria o acqua, facendolo oscillare al loro passaggio. Le onde del vento sono onde della superficie del mare che creano il caratteristico schema caotico di qualsiasi grande specchio d'acqua, sebbene il loro comportamento statistico possa essere previsto con i modelli delle onde del vento. Quando le onde nell'acqua o nel vento passano sulla sabbia, creano modelli di increspature. Quando i venti soffiano su grandi masse di sabbia, creano dune , a volte in vasti campi di dune come nel deserto di Taklamakan . Le dune possono formare una serie di modelli tra cui mezzelune, linee rette molto lunghe, stelle, cupole, parabole e forme longitudinali o seif ("spada").
Barchans o dune a mezzaluna sono prodotte dal vento che agisce sulla sabbia del deserto; le due corna della mezzaluna e la faccia scivolata puntano sottovento. La sabbia soffia sopra la parete di bolina, che si trova a circa 15 gradi dall'orizzontale, e cade sulla parete di scorrimento, dove si accumula fino all'angolo di riposo della sabbia, che è di circa 35 gradi. Quando la superficie di scivolamento supera l'angolo di riposo, le valanghe di sabbia , che è un comportamento non lineare : l'aggiunta di molte piccole quantità di sabbia non fa accadere molto, ma poi l'aggiunta di un'ulteriore piccola quantità provoca improvvisamente una grande quantità di valanga . A parte questa non linearità, i barchan si comportano piuttosto come onde solitarie .
Dune: dune di sabbia nel deserto di Taklamakan , dallo spazio
Dune: duna di sabbia a mezzaluna di Barchan
Increspature del vento con dislocazioni nel Sistan , Afghanistan
Bolle, schiuma
Una bolla di sapone forma una sfera , una superficie con un'area minima ( superficie minima ) — la superficie più piccola possibile per il volume racchiuso. Due bolle insieme formano una forma più complessa: le superfici esterne di entrambe le bolle sono sferiche; queste superfici sono unite da una terza superficie sferica poiché la bolla più piccola si gonfia leggermente in quella più grande.
Una schiuma è una massa di bolle; schiume di materiali diversi si trovano in natura. Le schiume composte da film di sapone obbediscono alle leggi di Plateau , che richiedono che tre film di sapone si incontrino a ciascun bordo a 120° e quattro bordi di sapone si incontrino a ciascun vertice con un angolo tetraedrico di circa 109,5°. Le leggi di Plateau richiedono inoltre che i film siano lisci e continui e che abbiano una curvatura media costante in ogni punto. Ad esempio, una pellicola può rimanere in media quasi piatta essendo curvata verso l'alto in una direzione (ad esempio, da sinistra a destra) mentre è curvata verso il basso in un'altra direzione (ad esempio, dalla parte anteriore a quella posteriore). Strutture con superfici minime possono essere utilizzate come tende.
Alla scala delle cellule viventi , i modelli di schiuma sono comuni; radiolari , spicole di spugna , esoscheletri di silicoflagellati e lo scheletro di calcite di un riccio di mare , Cidaris rugosa , assomigliano tutti a calchi minerali dei bordi della schiuma del Plateau. Lo scheletro del Radiolarian , Aulonia extenda , una bellissima forma marina disegnata da Ernst Haeckel , sembra una sfera composta interamente da esagoni, ma ciò è matematicamente impossibile. La caratteristica di Eulero afferma che per ogni poliedro convesso , il numero di facce più il numero di vertici (angoli) è uguale al numero di spigoli più due. Un risultato di questa formula è che qualsiasi poliedro chiuso di esagoni deve includere esattamente 12 pentagoni, come un pallone da calcio , una cupola geodetica di Buckminster Fuller o una molecola di fullerene . Questo può essere visualizzato osservando che una rete di esagoni è piatta come un foglio di rete metallica, ma ogni pentagono che viene aggiunto costringe la rete a piegarsi (ci sono meno angoli, quindi la rete viene tirata dentro).
Radiolaria disegnata da Haeckel nel suo Kunstformen der Natur (1904).
Spumellaria di Haeckel ; gli scheletri di questi Radiolari hanno forme schiumose.
Buckminsterfullerene C 60 : Richard Smalley e colleghi hanno sintetizzato la molecola del fullerene nel 1985.
I brochosomi ( microparticelle secretorie prodotte dalle cicaline ) spesso approssimano la geometria del fullerene .
tassellazioni
Le tassellazioni sono motivi formati dalla ripetizione di tessere su una superficie piana. Ci sono 17 gruppi di sfondi di piastrelle. Sebbene comuni nell'arte e nel design, le piastrelle esattamente ripetute sono meno facili da trovare negli esseri viventi. Esempi ben noti sono le celle nei nidi di carta delle vespe sociali , e le celle di cera in nido d' ape costruite dalle api mellifere. Tra gli animali, pesci ossei, rettili o il pangolino , o frutti come il salak sono protetti da squame sovrapposte o osteodermi , questi formano unità più o meno esattamente ripetitive, sebbene spesso le squame in realtà varino continuamente di dimensioni. Tra i fiori, la fritillary a testa di serpente, Fritillaria meleagris , ha un motivo a scacchiera a mosaico sui petali. Le strutture dei minerali forniscono buoni esempi di matrici tridimensionali che si ripetono regolarmente. Nonostante le centinaia di migliaia di minerali noti, esistono pochi tipi possibili di disposizione degli atomi in un cristallo , definita dalla struttura cristallina , sistema di cristallo , e gruppo di punti ; per esempio, ci sono esattamente 14 reticoli di Bravais per i 7 sistemi reticolari nello spazio tridimensionale.
Cristalli: cristalli cubici di salgemma (salgemma); sistema cristallino cubico , simmetria cristallina esottaedrica isometrica
Array: il nido d'ape è una tassellatura naturale
Cristallo a tramoggia di bismuto che illustra l'abito del cristallo a gradini .
Piastrelle: fiore a mosaico di testa di serpente fritillary, Fritillaria meleagris
Piastrelle: scaglie sovrapposte di triotto, Rutilus rutilus
Piastrelle: scaglie sovrapposte di frutta serpente o salak , Salacca zalacca
Pavimentazione tassellata : una rara formazione rocciosa nella penisola della Tasmania
crepe
Le crepe sono aperture lineari che si formano nei materiali per alleviare lo stress . Quando un materiale elastico si allunga o si restringe in modo uniforme, alla fine raggiunge la sua resistenza alla rottura e poi si rompe improvvisamente in tutte le direzioni, creando crepe con giunti di 120 gradi, quindi tre crepe si incontrano in un nodo. Al contrario, quando un materiale anelastico si rompe, si formano crepe diritte per alleviare lo stress. Ulteriori sollecitazioni nella stessa direzione aprirebbero semplicemente le crepe esistenti; sollecitazioni ad angolo retto possono creare nuove crepe, a 90 gradi rispetto a quelle vecchie. Quindi il modello delle crepe indica se il materiale è elastico o meno. In un materiale fibroso duro come la corteccia di quercia, si formano delle crepe per alleviare lo stress come al solito, ma non crescono finché la loro crescita è interrotta da fasci di forti fibre elastiche. Poiché ogni specie di albero ha la sua struttura a livello di cellula e di molecole, ognuna ha il suo schema di scissione nella sua corteccia.
Fango anelastico essiccante nel Rann of Kutch con fessure principalmente a 90°
Gabbro venato con fessure a 90°, vicino a Sgurr na Stri , Skye
Fango elastico essiccante in Sicilia con fessure prevalentemente a 120°
Basalto raffreddato a Giant's Causeway . Crepe verticali principalmente a 120° che danno colonne esagonali
Macchie, strisce
Si avvistano leopardi e coccinelle; pesci angelo e zebre sono a strisce. Questi modelli hanno una spiegazione evolutiva : hanno funzioni che aumentano le possibilità che la prole dell'animale modellato sopravviva per riprodursi. Una funzione dei modelli animali è il camuffamento ; per esempio, un leopardo più difficile da vedere cattura più prede. Un'altra funzione è la segnalazione : ad esempio, una coccinella ha meno probabilità di essere attaccata da uccelli predatori che cacciano a vista, se ha colori di avvertimento audaci, ed è anche sgradevolmente amara o velenosa o imita altri insetti sgradevoli. Un giovane uccello può vedere un insetto con un motivo di avvertimento come una coccinella e provare a mangiarlo, ma lo farà solo una volta; molto presto sputerà fuori l'insetto amaro; le altre coccinelle della zona rimarranno indisturbate. I giovani leopardi e coccinelle, ereditando geni che in qualche modo creano macchie, sopravvivono. Ma mentre questi argomenti evolutivi e funzionali spiegano perché questi animali hanno bisogno dei loro schemi, non spiegano come si formano i modelli.
Dirce bellezza farfalla, Colobura dirce
Zebra di Grevy , Equus grevyi
Pesce angelo reale , Pygoplites diacanthus
Leopardo , Panthera pardus pardus
Matrice di coccinelle di GG Jacobson
Modello di allevamento della seppia , Sepia officinalis
Formazione del modello
Alan Turing, e in seguito il biologo matematico James Murray , descrissero un meccanismo che crea spontaneamente schemi a macchie o strisce: un sistema di reazione-diffusione . Le cellule di un organismo giovane hanno geni che possono essere attivati da un segnale chimico, un morfogeno , che porta alla crescita di un certo tipo di struttura, diciamo una macchia di pelle scura. Se il morfogeno è presente ovunque, il risultato è una pigmentazione uniforme, come in un leopardo nero. Ma se è distribuito in modo non uniforme, possono risultare macchie o strisce. Turing ha suggerito che potrebbe esserci un controllo a feedback della produzione del morfogeno stesso. Ciò potrebbe causare continue fluttuazioni nella quantità di morfogeno che si diffonde nel corpo. È necessario un secondo meccanismo per creare modelli di onde stazionarie (per provocare macchie o strisce): un inibitore chimico che interrompe la produzione del morfogeno e che si diffonde attraverso il corpo più rapidamente del morfogeno, determinando uno schema attivatore-inibitore . La reazione Belousov-Zhabotinsky è un esempio non biologico di questo tipo di schema, un oscillatore chimico .
La ricerca successiva è riuscita a creare modelli convincenti di motivi diversi come strisce zebrate, macchie di giraffa, macchie di giaguaro (chiazze medio-scure circondate da anelli rotti scuri) e modelli di conchiglie di coccinelle (diverse disposizioni geometriche di macchie e strisce, vedi illustrazioni). I modelli di attivazione-inibizione di Richard Prum , sviluppati dal lavoro di Turing, utilizzano sei variabili per tenere conto della gamma osservata di nove modelli di pigmentazione di base all'interno delle penne, dal più semplice, una macchia di pigmento centrale, attraverso macchie concentriche, barre, chevron, occhi punto, coppia di punti centrali, file di punti accoppiati e una serie di punti. Modelli più elaborati simulano complessi modelli di piume nella faraona Numida meleagris in cui le singole piume presentano transizioni da barre alla base a una serie di punti all'estremità lontana (distale). Questi richiedono un'oscillazione creata da due segnali inibitori, con interazioni sia nello spazio che nel tempo.
I modelli possono formarsi per altri motivi nel paesaggio vegetato del cespuglio della tigre e delle onde di abete . Strisce di cespugli di tigre si verificano su pendii aridi dove la crescita delle piante è limitata dalle precipitazioni. Ogni striscia di vegetazione approssimativamente orizzontale raccoglie efficacemente l'acqua piovana dalla zona nuda immediatamente sopra di essa. Le onde di abete si verificano nelle foreste sui pendii montuosi dopo il disturbo del vento, durante la rigenerazione. Quando gli alberi cadono, gli alberi che avevano riparato diventano esposti e a loro volta hanno maggiori probabilità di essere danneggiati, quindi gli spazi vuoti tendono ad espandersi sottovento. Nel frattempo, sul lato sopravvento, crescono i giovani alberi, protetti dall'ombra del vento dei restanti alberi ad alto fusto. I modelli naturali sono talvolta formati da animali, come nei tumuli Mima degli Stati Uniti nordoccidentali e in alcune altre aree, che sembrano essere stati creati nel corso di molti anni dalle attività scavatrici dei roditori tascabili , mentre i cosiddetti circoli fatati della Namibia sembrano essere creato dall'interazione di gruppi concorrenti di termiti della sabbia, insieme alla competizione per l'acqua tra le piante del deserto.
Nei suoli di permafrost con uno strato superiore attivo soggetto a gelo e disgelo annuale, si può formare un terreno modellato , creando cerchi, reti, poligoni a cuneo di ghiaccio , gradini e strisce. La contrazione termica provoca la formazione di crepe da ritiro; in caso di disgelo, l'acqua riempie le fessure, espandendosi per formare ghiaccio quando viene successivamente congelata e allargando le fessure a spicchi. Queste crepe possono unirsi per formare poligoni e altre forme.
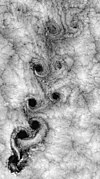
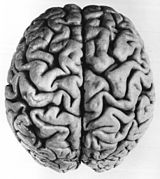
Il modello fessurata che si sviluppa su cervelli vertebrati è causato da un processo fisico di espansione vincolata dipendente da due parametri geometrici: espansione relativa corticale tangenziale e relativo spessore della corticale . Modelli simili di gyri (picchi) e solchi (avvallamenti) sono stati dimostrati in modelli del cervello a partire da gel lisci e stratificati, con i modelli causati da forze meccaniche di compressione risultanti dall'espansione dello strato esterno (che rappresenta la corteccia) dopo il aggiunta di un solvente. I modelli numerici nelle simulazioni al computer supportano osservazioni naturali e sperimentali che i modelli di piegatura della superficie aumentano nei cervelli più grandi.
Pesce palla gigante , Tetraodon mbu
Istantanea della simulazione della reazione di Belousov-Zhabotinsky
Faraona con elmo, Numida meleagris , le piume passano da barrate a maculate, sia in piuma che attraverso l'uccello
Vista aerea di un altopiano di Tiger Bush in Niger
Terreno modellato : un pingo in fusione con poligoni a cuneo di ghiaccio circostanti vicino a Tuktoyaktuk , Canada
Cerchi delle fate nella zona di Marienflusstal in Namibia
Guarda anche
- Biologia dello sviluppo
- Emergenza
- Storia evolutiva delle piante
- Matematica e arte
- morfogenesi
- Formazione del modello
- Modello Widmanstätten
Riferimenti
Note a piè di pagina
citazioni
Bibliografia
Autori pionieri
-
Fibonacci, Leonardo . Liber Abaci , 1202.
- ———— tradotto da Sigler, Liber Abaci di Laurence E. Fibonacci . Springer, 2002.
- Haeckel, Ernst . Kunstformen der Natur (Forme d'arte nella natura), 1899-1904.
- Thompson, D'Arcy Wentworth . Sulla crescita e sulla forma . Cambridge, 1917.
Libri generali
- Adam, John A. Matematica in natura: modelli di modellazione nel mondo naturale . Princeton University Press , 2006.
- Ball, Filippo (2009a). Nature's Patterns: un arazzo in tre parti. 1: Forme . La stampa dell'università di Oxford.
- Ball, Filippo (2009b). Nature's Patterns: un arazzo in tre parti. 2: Flusso . La stampa dell'università di Oxford.
- Ball, Filippo (2009c). Nature's Patterns: un arazzo in tre parti. 3. Filiali . La stampa dell'università di Oxford.
- Palla, Filippo. Modelli in natura . Chicago, 2016.
- Murphy, Pat e Neill, William. Dal disegno della natura . Libri di cronaca , 1993.
- Rothenberg, David (2011). Sopravvivenza del bello: arte, scienza ed evoluzione . Bloomsbury Press .
- Stevens, Peter S. (1974). Modelli in natura . Little, Brown & Co .
- Stewart, Ian (2001). Che forma ha un fiocco di neve? Numeri magici in natura . Weidenfeld & Nicolson .
Modelli dalla natura (come arte)
- Edmaier, Bernard. Modelli della Terra . Phaidon Press , 2007.
- Macnab, Maggie. Design by Nature: utilizzo di forme e principi universali nel design . Nuovi cavalieri, 2012.
- Nakamura, Shigeki. Pattern Sourcebook: 250 modelli ispirati alla natura. . Libri 1 e 2. Rockport, 2009.
- O'Neill, Polly. Superfici e trame: un Visual Sourcebook . Nero, 2008.
- Porter, Eliot e Gleick, James . Il caos della natura . Pinguino vichingo , 1990.