Coppia - Torque

coppia
Rapporto tra forza F , coppia τ , lineare moto p , e momento angolare L in un sistema che ha rotazione vincolata ad un solo piano (forze e momenti dovuti gravità e l'attrito non considerato).
Simboli comuni	${\displaystyle \tau}$, M
unità SI	N⋅m
Altre unità	libbra-forza-piedi , lbf pollice, ozf⋅in
In unità di base SI	kg⋅m 2 s −2
Dimensione	M L 2 T −2

Parte di una serie su
Meccanica classica
${\displaystyle {\textbf {F}}={\frac {d}{dt}}(m{\textbf {v}})}$ Seconda legge del moto
Storia Sequenza temporale libri di testo
Rami
Fondamenti
formulazioni
Argomenti principali
Rotazione
Scienziati
portale di fisica  Categoria
v T e

In fisica e meccanica , la coppia è l'equivalente rotazionale della forza lineare . Viene anche chiamato momento , momento di forza , forza di rotazione o effetto di svolta , a seconda del campo di studio. Il concetto è nato dagli studi di Archimede sull'uso delle leve . Proprio come una forza lineare è una spinta o una trazione, una coppia può essere pensata come una torsione di un oggetto attorno a un asse specifico. Altra definizione di momento torcente è prodotto del modulo della forza per la distanza perpendicolare della retta d'azione di una forza dall'asse di rotazione . Il simbolo per la coppia è in genere o τ , il minuscolo lettera greca tau . Quando viene indicato come momento della forza, è comunemente indicato con M . ${\displaystyle {\boldsymbol {\tau}}}$

In tre dimensioni, la coppia è uno pseudovettore ; per le particelle puntiformi è data dal prodotto vettoriale del vettore posizione ( vettore distanza ) e del vettore forza. L'entità della coppia di un corpo rigido dipende da tre grandezze: la forza applicata, il vettore del braccio di leva che collega il punto attorno al quale viene misurata la coppia al punto di applicazione della forza e l'angolo tra la forza e i vettori del braccio di leva. Nei simboli:

${\displaystyle {\boldsymbol {\tau}}=\mathbf {r} \times \mathbf {F} \,\!}$

${\displaystyle \tau =\|\mathbf {r} \|\,\|\mathbf {F} \|\sin \theta \,\!}$

dove

${\displaystyle {\boldsymbol {\tau}}}$è il vettore della coppia ed è il modulo della coppia,${\displaystyle \tau}$

${\displaystyle \mathbf {r}}$ è il vettore posizione (un vettore dal punto attorno al quale viene misurata la coppia al punto in cui viene applicata la forza),

${\displaystyle \mathbf {F}}$ è il vettore della forza,

${\displaystyle \times}$denota il prodotto vettoriale , che produce un vettore perpendicolare sia a r che a F seguendo la regola della mano destra ,

${\displaystyle \theta}$ è l'angolo tra il vettore della forza e il vettore del braccio di leva.

L' unità SI per la coppia è il newton-metro (N⋅m). Per ulteriori informazioni sulle unità di coppia, vedere § Unità .

Definire la terminologia

James Thomson , il fratello di Lord Kelvin , introdusse il termine torque nella letteratura scientifica inglese nel 1884. Tuttavia, il termine torque viene indicato utilizzando un vocabolario diverso a seconda della posizione geografica e del campo di studio. Questo articolo segue la definizione utilizzata nella fisica statunitense nell'uso della parola coppia . Nel Regno Unito e nell'ingegneria meccanica statunitense , la coppia viene definita momento della forza , solitamente accorciato al momento . Questi termini sono intercambiabili nella terminologia fisica degli Stati Uniti e della fisica del Regno Unito, a differenza dell'ingegneria meccanica degli Stati Uniti, dove il termine coppia è usato per il "momento risultante di una coppia " strettamente correlato .

Coppia e momento nella terminologia dell'ingegneria meccanica statunitense

Nell'ingegneria meccanica statunitense, la coppia è definita matematicamente come la velocità di variazione del momento angolare di un oggetto (in fisica è chiamata "coppia netta"). La definizione di coppia afferma che una o entrambe le velocità angolari o il momento d'inerzia di un oggetto stanno cambiando. Momento è il termine generale usato per la tendenza di una o più forze applicate a ruotare un oggetto attorno a un asse, ma non necessariamente a cambiare il momento angolare dell'oggetto (il concetto che in fisica è chiamato coppia ). Ad esempio, una forza di rotazione applicata a un albero che causa accelerazione, come una punta da trapano che accelera da fermo, si traduce in un momento chiamato coppia . Al contrario, una forza laterale su una trave produce un momento (chiamato momento flettente ), ma poiché il momento angolare della trave non cambia, questo momento flettente non è chiamato coppia . Allo stesso modo, con qualsiasi coppia di forze su un oggetto che non cambia il suo momento angolare, anche tale momento non è chiamato coppia .

Definizione e relazione con il momento angolare

Una particella si trova nella posizione r rispetto al suo asse di rotazione. Quando una forza F viene applicata alla particella, solo la componente perpendicolare F _⊥ produce una coppia. Questa coppia τ  =  r  ×  F ha modulo τ  = | r | | F _⊥ | = | r | | F | sin θ ed è diretto verso l'esterno dalla pagina.

Una forza applicata perpendicolarmente a una leva moltiplicata per la sua distanza dal fulcro della leva (la lunghezza del braccio di leva ) è la sua coppia. Una forza di tre newton applicata a due metri dal fulcro, ad esempio, esercita la stessa coppia di una forza di un newton applicata a sei metri dal fulcro. La direzione della coppia può essere determinata utilizzando la regola della presa della mano destra : se le dita della mano destra sono piegate dalla direzione del braccio di leva alla direzione della forza, allora il pollice punta nella direzione della coppia.

Più in generale, la coppia su una particella puntiforme (che ha la posizione r in qualche sistema di riferimento) può essere definita come il prodotto vettoriale :

${\displaystyle {\boldsymbol {\tau}}=\mathbf {r} \times \mathbf {F},}$

dove r è il vettore di posizione della particella rispetto al fulcro e F è la forza che agisce sulla particella. Il modulo della coppia è dato da

${\displaystyle \tau =rF\sin \theta ,\!}$

dove r è la distanza dall'asse di rotazione alla particella, F è la grandezza della forza applicata, e θ è l'angolo tra i vettori di posizione e forza. In alternativa,

${\displaystyle \tau =rF_{\perp },}$

dove F _⊥ è la quantità di forza diretta perpendicolarmente alla posizione della particella. Qualsiasi forza diretta parallela al vettore di posizione della particella non produce una coppia.

Dalle proprietà del prodotto vettoriale segue che il vettore di coppia è perpendicolare sia al vettore di posizione che a quello di forza . Viceversa, il vettore coppia definisce il piano in cui giacciono i vettori posizione e forza . La direzione del vettore di coppia risultante è determinata dalla regola della mano destra.

La coppia netta su un corpo determina la velocità di variazione del momento angolare del corpo ,

${\ Displaystyle {\ Boldsymbol {\ tau}} = {\ frac {\ mathrm {d} \ mathbf {L}} {\ mathrm {d} t}}}$

dove L è il vettore del momento angolare e t è il tempo.

Per il moto di una particella puntiforme,

${\displaystyle \mathbf {L} =I{\boldsymbol {\omega }},}$

dove I è il momento di inerzia e ω è la orbitale velocità angolare pseudovettore. Ne consegue che

${\displaystyle {\boldsymbol {\tau }}_{\mathrm {rete}}={\frac {\mathrm {d} \mathbf {L}}}{\mathrm {d} t}}={\frac {\ mathrm {d} (I{\boldsymbol {\omega }})}{\mathrm {d} t}}=I{\frac {\mathrm {d} {\boldsymbol {\omega}}}{\mathrm {d } t}}+{\frac {\mathrm {d} I}{\mathrm {d} t}}{\boldsymbol {\omega }}=I{\boldsymbol {\alpha }}+{\frac {\mathrm {d} (mr^{2})}{\mathrm {d} t}}{\boldsymbol {\omega }}=I{\boldsymbol {\alpha }}+2rp_{||}{\boldsymbol {\omega }},}$

dove α è l' accelerazione angolare della particella, e p _|| è la componente radiale del suo momento lineare . Questa equazione è l'analogo rotazionale della Seconda Legge di Newton per le particelle puntiformi ed è valida per qualsiasi tipo di traiettoria. Si noti che anche se la forza e l'accelerazione sono sempre paralleli e direttamente proporzionale alla coppia τ non deve essere parallelo o direttamente proporzionale all'accelerazione angolare α . Ciò deriva dal fatto che sebbene la massa sia sempre conservata, il momento d'inerzia in generale non lo è.

Prova dell'equivalenza delle definizioni

La definizione di momento angolare per una particella a punto singolo è:

${\displaystyle \mathbf {L} =\mathbf {r} \times {\boldsymbol {p}}}$

dove p è il momento lineare della particella e r è il vettore posizione dall'origine. La derivata temporale di questo è:

${\displaystyle {\frac {\mathrm {d} \mathbf {L} }{\mathrm {d} t}}=\mathbf {r} \times {\frac {\mathrm {d} {\boldsymbol {p} }}{\mathrm {d} t}}+{\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}\times {\boldsymbol {p}}.}$

Questo risultato può essere facilmente dimostrato suddividendo i vettori in componenti e applicando la regola del prodotto . Ora usando la definizione di forza (se la massa è costante o meno) e la definizione di velocità${\displaystyle \mathbf {F} ={\frac {\mathrm {d} {\boldsymbol {p}}}{\mathrm {d} t}}}$${\displaystyle {\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}=\mathbf {v} }$

${\displaystyle {\frac {\mathrm {d} \mathbf {L} }{\mathrm {d} t}}=\mathbf {r} \times \mathbf {F} +\mathbf {v} \times {\ simbolo in grassetto {p}}.}$

Il prodotto vettoriale della quantità di moto con la sua velocità associata è zero perché velocità e quantità di moto sono parallele, quindi il secondo termine svanisce. ${\displaystyle {\boldsymbol {p}}}$${\displaystyle \mathbf {v}}$

Per definizione, coppia τ = r × F . Pertanto, la coppia su una particella è uguale alla derivata prima del suo momento angolare rispetto al tempo.

Se vengono applicate più forze, la seconda legge di Newton legge invece F _net = m a , e ne segue che

${\displaystyle {\frac {\mathrm {d} \mathbf {L} }{\mathrm {d} t}}=\mathbf {r} \times \mathbf {F} _{\mathrm {net} }={ \boldsymbol {\tau }}_{\mathrm {rete} }.}$

Questa è una prova generale per le particelle puntiformi.

La dimostrazione può essere generalizzata a un sistema di particelle puntiformi applicando la dimostrazione di cui sopra a ciascuna delle particelle puntiformi e quindi sommando su tutte le particelle puntiformi. Allo stesso modo, la dimostrazione può essere generalizzata a una massa continua applicando la dimostrazione di cui sopra a ciascun punto all'interno della massa e quindi integrando sull'intera massa.

Unità

La coppia ha la dimensione della forza per la distanza , simbolicamente T ⁻² L ² M . Sebbene queste dimensioni fondamentali siano le stesse dell'energia o del lavoro , la letteratura ufficiale del SI suggerisce di utilizzare l'unità newton metro (N⋅m) e mai il joule . L'unità newton metro è correttamente indicata con N⋅m.

Le unità tradizionali imperiali e statunitensi per la coppia sono il piede libbra (lbf-ft) o per valori piccoli il pollice libbra (lbf-in). Negli Stati Uniti, la coppia è più comunemente indicata come piede per libbra (denotato come lb-ft o ft-lb) e pollice-libbra (denotato come in-lb). I praticanti dipendono dal contesto e dal trattino nell'abbreviazione per sapere che questi si riferiscono alla coppia e non all'energia o al momento della massa (come implicherebbe correttamente il simbolismo ft-lb).

Casi speciali e altri fatti

Formula braccio momento

Diagramma del braccio del momento

Un caso speciale molto utile, spesso dato come definizione di momento torcente in campi diversi dalla fisica, è il seguente:

${\displaystyle \tau =({\text{momento braccio}})({\text{forza}}).}$

La costruzione del "braccio momento" è mostrata nella figura a destra, insieme ai vettori r e F sopra menzionati. Il problema con questa definizione è che non dà la direzione della coppia ma solo la grandezza, e quindi è difficile da usare nei casi tridimensionali. Se la forza è perpendicolare al vettore spostamento r , il braccio del momento sarà uguale alla distanza dal centro e la coppia sarà un massimo per la forza data. L'equazione per la grandezza di una coppia, derivante da una forza perpendicolare:

${\displaystyle \tau =({\text{distanza dal centro}})({\text{forza}}).}$

Ad esempio, se una persona applica una forza di 10 N all'estremità terminale di una chiave lunga 0,5 m (o una forza di 10 N esattamente 0,5 m dal punto di torsione di una chiave di qualsiasi lunghezza), la coppia sarà 5 N⋅m – supponendo che la persona muova la chiave applicando una forza nel piano di movimento e perpendicolare alla chiave.

La coppia causata dalle due forze opposte F _g e − F _g provoca una variazione del momento angolare L nella direzione di quella coppia. Ciò provoca la precessione della parte superiore .

Equilibrio statico

Affinché un oggetto sia in equilibrio statico , non solo la somma delle forze deve essere zero, ma anche la somma dei momenti (momenti) attorno a qualsiasi punto. Per una situazione bidimensionale con forze orizzontali e verticali, la somma delle forze richieste è due equazioni: Σ H = 0 e Σ V = 0, e la coppia una terza equazione: Σ τ = 0. Cioè, per risolvere staticamente determinati problemi di equilibrio in due dimensioni, vengono utilizzate tre equazioni.

Forza netta contro coppia

Quando la forza netta sul sistema è zero, la coppia misurata da qualsiasi punto nello spazio è la stessa. Ad esempio, la coppia su un circuito percorso da corrente in un campo magnetico uniforme è la stessa indipendentemente dal punto di riferimento. Se la forza netta non è zero, ed è la coppia misurata da , allora la coppia misurata da è ${\displaystyle \mathbf {F}}$${\displaystyle {\boldsymbol {\tau}}_{1}}$${\displaystyle \mathbf {r} _{1}}$${\displaystyle \mathbf {r} _{2}}$

$${\displaystyle {\boldsymbol {\tau}}_{2}={\boldsymbol {\tau}}_{1}+(\mathbf {r} _{1}-\mathbf {r} _{2}) \times \mathbf {F} }$$

Coppia macchina

Curva di coppia di una moto ("BMW K 1200 R 2005"). L'asse orizzontale mostra la velocità (in giri/min ) che l' albero motore sta girando, e l'asse verticale è la coppia (in newton metri ) che il motore è in grado di fornire a quel regime.

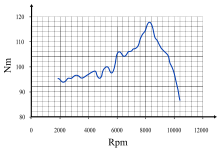
La coppia fa parte delle specifiche di base di un motore : la potenza erogata da un motore è espressa come la sua coppia moltiplicata per la sua velocità di rotazione dell'asse. I motori a combustione interna producono una coppia utile solo in un intervallo limitato di velocità di rotazione (tipicamente da circa 1.000 a 6.000 giri/min per una piccola auto). Si può misurare la variazione di coppia erogata su tale intervallo con un dinamometro e mostrarla come una curva di coppia.

I motori a vapore e i motori elettrici tendono a produrre una coppia massima prossima allo zero giri/min, con la coppia che diminuisce all'aumentare della velocità di rotazione (a causa dell'aumento dell'attrito e di altri vincoli). Motori alternativi a vapore e motori elettrici possono avviare carichi pesanti da zero giri/min senza frizione .

Relazione tra coppia, potenza ed energia

Se una forza può agire attraverso una distanza, sta facendo un lavoro meccanico . Allo stesso modo, se la coppia può agire attraverso una distanza di rotazione, sta funzionando. Matematicamente, per la rotazione attorno ad un asse fisso passante per il centro di massa , il lavoro W può essere espresso come

${\displaystyle W=\int _{\theta _{1}}^{\theta _{2}}\tau \ \mathrm {d} \theta ,}$

dove τ è la coppia, e θ ₁ e θ ₂ rappresentano (rispettivamente) le iniziali e finali posizioni angolari del corpo.

Prova

Il lavoro compiuto da una forza variabile che agisce su uno spostamento lineare finito è dato integrando la forza rispetto a uno spostamento lineare elementare${\displaystyle}$${\displaystyle \mathrm {d} \mathbf {s} }$

${\displaystyle W=\int _{s_{1}}^{s_{2}}\mathbf {F} \cdot \mathrm {d} \mathbf {s} }$

Tuttavia, lo spostamento lineare infinitesimale è correlato a un corrispondente spostamento angolare e il raggio vettore as ${\displaystyle \mathrm {d} \mathbf {s} }$${\displaystyle \mathrm {d} {\boldsymbol {\theta}}}$${\displaystyle \mathbf {r}}$

${\displaystyle \mathrm {d} \mathbf {s} =\mathrm {d} {\boldsymbol {\theta}}\times \mathbf {r}}$

La sostituzione nell'espressione sopra per lavoro dà

${\displaystyle W=\int _{s_{1}}^{s_{2}}\mathbf {F} \cdot \mathrm {d} {\boldsymbol {\theta}}\times \mathbf {r}}$

L'espressione è un prodotto triplo scalare dato da . Un'espressione alternativa per lo stesso prodotto triplo scalare è ${\displaystyle \mathbf {F} \cdot \mathrm {d} {\boldsymbol {\theta}}\times \mathbf {r}}$${\displaystyle \left[\mathbf {F} \,\mathrm {d} {\boldsymbol {\theta}}\,\mathbf {r} \right]}$

${\displaystyle \left[\mathbf {F} \,\mathrm {d} {\boldsymbol {\theta}}\,\mathbf {r} \right]=\mathbf {r} \times \mathbf {F} \ cdot \mathrm {d} {\boldsymbol {\theta}}}$

Ma secondo la definizione di coppia,

${\displaystyle {\boldsymbol {\tau}}=\mathbf {r} \times \mathbf {F}}$

La corrispondente sostituzione nell'espressione del lavoro dà,

${\displaystyle W=\int _{s_{1}}^{s_{2}}{\boldsymbol {\tau }}\cdot \mathrm {d} {\boldsymbol {\theta}}}$

Poiché il parametro di integrazione è stato modificato da spostamento lineare a spostamento angolare, anche i limiti dell'integrazione cambiano di conseguenza, dando

${\displaystyle W=\int _{\theta _{1}}^{\theta _{2}}{\boldsymbol {\tau }}\cdot \mathrm {d} {\boldsymbol {\theta}}}$

Se la coppia e lo spostamento angolare sono nella stessa direzione, allora il prodotto scalare si riduce a un prodotto di grandezze; cioè, dare ${\displaystyle {\boldsymbol {\tau}}\cdot \mathrm {d} {\boldsymbol {\theta}}=\left|{\boldsymbol {\tau}}\right|\left|\mathrm {d} { \boldsymbol {\theta}}\right|\cos 0=\tau \,\mathrm {d} \theta}$

${\displaystyle W=\int _{\theta _{1}}^{\theta _{2}}\tau \,\mathrm {d} \theta }$

Dal teorema lavoro-energia segue che W rappresenta anche la variazione dell'energia cinetica rotazionale E _r del corpo, data da

${\displaystyle E_{\mathrm {r} }={\tfrac {1}{2}}Io\omega ^{2},}$

dove I è il momento di inerzia del corpo e ω è la sua velocità angolare .

La potenza è il lavoro per unità di tempo , dato da

${\displaystyle P={\boldsymbol {\tau}}\cdot {\boldsymbol {\omega}},}$

dove P è la potenza, τ è coppia, ω è la velocità angolare , e rappresenta il prodotto scalare . ${\displaystyle \cdot}$

Algebricamente, l'equazione può essere riorganizzata per calcolare la coppia per una data velocità angolare e potenza. Si noti che la potenza iniettata dalla coppia dipende solo dalla velocità angolare istantanea, non dal fatto che la velocità angolare aumenti, diminuisca o rimanga costante mentre viene applicata la coppia (questo è equivalente al caso lineare in cui la potenza iniettata da una forza dipende solo dalla velocità istantanea, non dall'eventuale accelerazione risultante).

In pratica, questa relazione può essere osservata nelle biciclette : le biciclette sono tipicamente composte da due ruote da strada, ingranaggi anteriori e posteriori (denominati pignoni ) che ingranano con una catena circolare e un meccanismo a deragliatore se il sistema di trasmissione della bicicletta consente rapporti di trasmissione multipli da utilizzare (es. bicicletta multivelocità ), il tutto agganciato al telaio . Un ciclista , la persona che guida la bicicletta, fornisce la potenza in ingresso girando i pedali, facendo così girare la ruota dentata anteriore (comunemente denominata corona ). La potenza in ingresso fornita dal ciclista è pari al prodotto della cadenza (cioè il numero di giri del pedale al minuto) e la coppia sul perno della guarnitura della bicicletta . La trasmissione della bicicletta trasmette la potenza in ingresso alla ruota da strada , che a sua volta trasmette la potenza ricevuta alla strada come potenza in uscita dalla bicicletta. A seconda del rapporto di trasmissione della bicicletta, una coppia di _input (coppia, giri/min) viene convertita in una coppia di _output (coppia, giri/min) . Utilizzando una marcia posteriore più grande, o passando a una marcia più bassa nelle biciclette a più velocità, la velocità angolare delle ruote stradali viene ridotta mentre viene aumentata la coppia, il cui prodotto (cioè la potenza) non cambia.

È necessario utilizzare unità coerenti. Per le unità metriche SI, la potenza è watt , la coppia è newton metri e la velocità angolare è radianti al secondo (non giri/min e non giri al secondo).

Inoltre, l'unità newton metro è dimensionalmente equivalente al joule , che è l'unità di misura dell'energia. Tuttavia, nel caso della coppia, l'unità è assegnata a un vettore , mentre per l' energia è assegnata a uno scalare . Ciò significa che l'equivalenza dimensionale del newtonmetro e del joule può essere applicata nel primo caso, ma non nel secondo. Questo problema è affrontato nell'analisi orientativa che tratta i radianti come un'unità di base piuttosto che come un'unità adimensionale.

Conversione in altre unità

Potrebbe essere necessario un fattore di conversione quando si utilizzano diverse unità di potenza o coppia. Ad esempio, se la velocità di rotazione (giri al tempo) è utilizzato al posto della velocità angolare (radianti al tempo), abbiamo moltiplicare per un fattore di 2 ¸ radianti per giro. Nelle seguenti formule, P è la potenza, τ è coppia, e ν ( lettera greca nu ) è la velocità di rotazione.

${\displaystyle P=\tau\cdot 2\pi \cdot \nu}$

Visualizzazione delle unità:

${\displaystyle P({\rm {W}})=\tau {\rm {(N\cdot m)}}\cdot 2\pi {\rm {(rad/rev)}}\cdot \nu {\ rm {(giri/sec)}}}$

Dividendo per 60 secondi al minuto si ottiene quanto segue.

${\displaystyle P({\rm {W}})={\frac {\tau {\rm {(N\cdot m)}}\cdot 2\pi {\rm {(rad/rev)}}\cdot \nu {\rm {(rpm)}}}{60}}}$

dove la velocità di rotazione è espressa in giri al minuto (rpm).

Alcune persone (ad esempio, gli ingegneri automobilistici americani) usano la potenza (meccanica) per la potenza, i piedi per libbra (lbf⋅ft) per la coppia e il numero di giri per la velocità di rotazione. Ciò comporta la modifica della formula in:

${\displaystyle P({\rm {hp}})={\frac {\tau {\rm {(lbf\cdot ft)}}\cdot 2\pi {\rm {(rad/rev)}}\cdot \nu ({\rm {rpm}})}{33.000}}.}$

La costante sottostante (in piedi per libbra al minuto) cambia con la definizione della potenza; ad esempio, utilizzando la potenza metrica, diventa circa 32.550.

L'uso di altre unità (ad es. BTU all'ora per l'alimentazione) richiederebbe un diverso fattore di conversione personalizzato.

Derivazione

Per un oggetto rotante, la distanza lineare coperta alla circonferenza di rotazione è il prodotto del raggio con l'angolo coperto. Cioè: distanza lineare = raggio × distanza angolare. E per definizione, distanza lineare = velocità lineare × tempo = raggio × velocità angolare × tempo.

Per definizione di coppia: coppia = raggio × forza. Possiamo riorganizzare questo per determinare forza = coppia ÷ raggio. Questi due valori possono essere sostituiti nella definizione di potenza :

${\displaystyle {\begin{aligned}{\text{power}}&={\frac {{\text{force}}\cdot {\text{distanza lineare}}}{\text{time}}}\\ [6pt]&={\frac {\left({\dfrac {\text{coppia}}{r}}\right)\cdot (r\cdot {\text{velocità angolare}}\cdot t)}{t }}\\[6pt]&={\text{coppia}}\cdot {\text{velocità angolare}}.\end{allineato}}}$

Il raggio r e il tempo t sono usciti dall'equazione. Tuttavia, la velocità angolare deve essere espressa in radianti per unità di tempo, per la presunta relazione diretta tra velocità lineare e velocità angolare all'inizio della derivazione. Se la velocità di rotazione è misurata in giri per unità di tempo, la velocità lineare e la distanza sono aumentati in proporzione da 2 π nella derivazione sopra per dare:

${\displaystyle {\text{potenza}}={\text{coppia}}\cdot 2\pi \cdot {\text{velocità di rotazione}}.\,}$

Se la coppia è in newton metri e la velocità di rotazione in giri al secondo, l'equazione di cui sopra fornisce la potenza in newton metri al secondo o watt. Se vengono utilizzate unità imperiali e se la coppia è espressa in libbre-forza piedi e la velocità di rotazione in giri al minuto, l'equazione di cui sopra fornisce la potenza in piedi libbre-forza al minuto. La forma della potenza dell'equazione viene quindi derivata applicando il fattore di conversione 33.000 ft⋅lbf/min per cavallo:

${\displaystyle {\begin{allineato}{\text{potenza}}&={\text{coppia}}\cdot 2\pi \cdot {\text{velocità di rotazione}}\cdot {\frac {{\text{ ft}}\cdot {\text{lbf}}}{\text{min}}}\cdot {\frac {\text{horsepower}}{33.000\cdot {\frac {{\text{ft}}\cdot {\text{lbf}}}{\text{min}}}}}\\[6pt]&\circa {\frac {{\text{coppia}}\cdot {\text{RPM}}}{5,252} }\end{allineato}}}$

perché ${\displaystyle 5252.113122\circa {\frac {33.000}{2\pi }}.\,}$

Principio dei momenti

Il Principio dei Momenti, noto anche come teorema di Varignon (da non confondere con l' omonimo teorema geometrico ) afferma che la somma dei momenti dovuti a più forze applicate ad un unico punto è uguale al momento dovuto alla somma (risultante ) delle forze. Matematicamente, questo segue da:

${\displaystyle (\mathbf {r} \times \mathbf {F} _{1})+(\mathbf {r} \times \mathbf {F} _{2})+\cdots =\mathbf {r} \ volte (\mathbf {F} _{1}+\mathbf {F} _{2}+\cdots ).}$

Da ciò ne consegue che se un raggio imperniato di massa zero è bilanciato con due forze opposte allora:

${\displaystyle (\mathbf {r} \times \mathbf {F} _{1})=(\mathbf {r} \times \mathbf {F} _{2}).}$

Moltiplicatore di coppia

La coppia può essere moltiplicata in tre modi: posizionando il fulcro in modo tale da aumentare la lunghezza di una leva; utilizzando una leva più lunga; o mediante l'uso di un riduttore di velocità o di una scatola del cambio . Tale meccanismo moltiplica la coppia, poiché la velocità di rotazione viene ridotta.

Guarda anche

Riferimenti

link esterno

• "Potenza e coppia" Un articolo che mostra come potenza, coppia e cambio influiscano sulle prestazioni di un veicolo.
• "Coppia contro potenza: ancora un altro argomento" Una prospettiva automobilistica
• Coppia e momento angolare in moto circolare sul progetto PHYSNET .
• Una simulazione interattiva della coppia
• Convertitore di unità di coppia
• Una sensazione per la coppia Un ordine di grandezza interattivo.