Triangolo di Keplero -Kepler triangle

Un triangolo di Keplero è un triangolo rettangolo speciale con lunghezze dei bordi in progressione geometrica . Il rapporto della progressione è dove si trova il rapporto aureo e la progressione può essere scritta: , o approssimativamente . I quadrati sui bordi di questo triangolo hanno aree in un'altra progressione geometrica, . Definizioni alternative dello stesso triangolo lo caratterizzano in termini di tre mezzi pitagorici di due numeri, o tramite l' inradius dei triangoli isoscele . ${\ displaystyle {\ sqrt {\ varphi}}}$${\displaystyle \varphi =(1+{\sqrt {5}})/2}$${\ displaystyle 1: {\ sqrt {\ varphi}}: \ varphi}$${\ displaystyle 1:1.272:1.618}$${\displaystyle 1:\varphi :\varphi ^{2}}$

Questo triangolo prende il nome da Johannes Kepler , ma può essere trovato in fonti precedenti. Sebbene alcune fonti affermino che le antiche piramidi egiziane avessero proporzioni basate su un triangolo di Keplero, la maggior parte degli studiosi ritiene che il rapporto aureo non fosse noto alla matematica e all'architettura egiziana.

Storia

Il triangolo di Kepler prende il nome dal matematico e astronomo tedesco Johannes Kepler (1571–1630), che scrisse di questa forma in una lettera del 1597. Due concetti che possono essere usati per analizzare questo triangolo, il teorema di Pitagora e il rapporto aureo, erano entrambi di interesse per Keplero, come scrisse altrove:

La geometria ha due grandi tesori: uno è il teorema di Pitagora, l'altro la divisione di una retta in rapporti estremi e medi. La prima la possiamo paragonare a una massa d'oro, la seconda la chiamiamo un gioiello prezioso.

Tuttavia, Keplero non è stato il primo a descrivere questo triangolo. Lo stesso Keplero lo attribuì a "un professore di musica di nome Magirus". Lo stesso triangolo compare in precedenza in un libro di matematica araba , il Liber mensurationum di Abû Bekr, noto da una traduzione del XII secolo di Gerardo da Cremona in latino, e nella Practica geometriae  [ it ] di Fibonacci (pubblicata nel 1220–1221) , che lo definì in modo simile a Keplero. Un po' prima di Keplero ne scrisse Pedro Nunes nel 1567, ed è "probabile che fosse diffuso nelle tradizioni manoscritte tardo medievali e rinascimentali". È stato anche riscoperto in modo indipendente più volte, più tardi di Keplero.

Secondo alcuni autori, una piramide d'oro con un triangolo di Keplero raddoppiato come sezione trasversale descrive accuratamente il design delle piramidi egiziane come la Grande Piramide di Giza ; una fonte di questa teoria è una lettura errata di Erodoto del XIX secolo da parte del piramidale John Taylor. Molte altre teorie della proporzione sono state proposte per la stessa piramide, estranea al triangolo di Keplero. Poiché queste diverse teorie sono molto simili nei valori numerici che ottengono e a causa delle imprecisioni nelle misurazioni, in parte causate dalla distruzione della superficie esterna della piramide, tali teorie sono difficili da risolvere sulla base di prove puramente fisiche. La corrispondenza delle proporzioni con il triangolo di Keplero potrebbe benissimo essere una coincidenza numerica: secondo gli studiosi che hanno studiato questa relazione, gli antichi egizi molto probabilmente non conoscevano o usavano il rapporto aureo nella loro matematica o architettura. Invece, le proporzioni della piramide possono essere adeguatamente spiegate usando rapporti interi, basati su un triangolo rettangolo con lati 11 e 14.

Il nome "Triangolo di Keplero" per questa forma è stato utilizzato da Roger Herz-Fischler, basato sulla lettera di Keplero del 1597, già nel 1979. Un altro nome per lo stesso triangolo, usato da Matila Ghyka nel suo libro del 1946 sul rapporto aureo, The Geometry di Arte e Vita , è il "triangolo di Price", dal piramidale WA Price.

Definizioni

Il triangolo di Keplero è definito in modo univoco dalle proprietà di essere un triangolo rettangolo e di avere le sue lunghezze laterali in progressione geometrica, o equivalentemente avere i quadrati ai suoi lati in progressione geometrica. Il rapporto tra la progressione delle lunghezze dei lati è , dove è il rapporto aureo , e la progressione può essere scritta: , o approssimativamente 1 : 1.272 : 1.618. I quadrati sui bordi di questo triangolo hanno aree in un'altra progressione geometrica, . Il fatto che il triangolo con queste proporzioni sia un triangolo rettangolo deriva dal fatto che, per lunghezze degli spigoli al quadrato con queste proporzioni, il polinomio che definisce il rapporto aureo è lo stesso della formula data dal teorema di Pitagora per le lunghezze degli spigoli al quadrato di un triangolo rettangolo: ${\ displaystyle {\ sqrt {\ varphi}}}$${\displaystyle \varphi =(1+{\sqrt {5}})/2}$${\ displaystyle 1: {\ sqrt {\ varphi}}: \ varphi}$${\displaystyle 1:\varphi :\varphi ^{2}}$

Poiché questa equazione è vera per il rapporto aureo, queste tre lunghezze obbediscono al teorema di Pitagora e formano un triangolo rettangolo. Al contrario, in qualsiasi triangolo rettangolo le cui lunghezze degli spigoli quadrati sono in progressione geometrica con qualsiasi rapporto , il teorema di Pitagora implica che questo rapporto obbedisce all'identità . Pertanto, il rapporto deve essere l'unica soluzione positiva a questa equazione, il rapporto aureo e il triangolo deve essere un triangolo di Keplero. ${\ displaystyle \ rho}$${\displaystyle \rho ^{2}=\rho +1}$

Le tre lunghezze degli spigoli e sono rispettivamente la media armonica , la media geometrica e la media aritmetica dei due numeri . Questi tre modi di combinare due numeri furono tutti studiati nell'antica matematica greca e sono chiamati mezzi pitagorici . Al contrario, questa può essere presa come una definizione alternativa del triangolo di Keplero: è un triangolo rettangolo le cui lunghezze degli spigoli sono le tre medie pitagoriche di due numeri. Gli unici triangoli per i quali questo è vero sono i triangoli di Keplero. ${\ displaystyle 1}$${\ displaystyle {\ sqrt {\ varphi}}}$${\ displaystyle \ varphi}$${\ displaystyle \ varphi \ pm 1}$

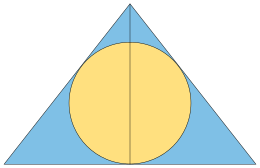
Un terzo modo equivalente di definire questo triangolo deriva da un problema di massimizzare il raggio interno dei triangoli isoscele . Tra tutti i triangoli isoscele con una scelta fissa della lunghezza dei due lati uguali ma con una lunghezza di base variabile, quello con il raggio di apertura maggiore è formato da due copie del triangolo di Keplero, riflesse l'una dall'altra sul loro bordo più corto. Pertanto, il triangolo di Keplero può essere definito come il triangolo rettangolo che, tra tutti i triangoli rettangoli con la stessa ipotenusa, forma con la sua riflessione il triangolo isoscele di raggio massimo. Quando il triangolo di Keplero si riflette sul più lungo dei suoi due lati perpendicolari, forma invece il triangolo isoscele che, per un dato perimetro, contiene il semicerchio più grande possibile .

Proprietà

Se il lato corto di un triangolo di Keplero ha lunghezza , gli altri lati avranno lunghezze e . L'area può essere calcolata con la formula standard per l'area dei triangoli rettangoli (metà del prodotto dei due lati corti) come . Il coseno del maggiore dei due angoli non retti è il rapporto tra il lato adiacente (il più corto dei due lati) e l'ipotenusa, da cui segue che i due angoli non retti sono ${\ displaystyle s}$${\ displaystyle s {\ sqrt {\ varphi}}}$${\ displaystyle s \ varphi}$${\displaystyle {\tfrac {s^{2}}{2}}{\sqrt {\varphi}}}$${\ displaystyle \ varphi}$

e

Jerzy Kocik ha osservato che il maggiore di questi due angoli è anche l'angolo formato dai centri di triple di cerchi consecutivi nella sequenza loxodromica di cerchi tangenti di Coxeter .

Guarda anche

• Triangolo automediano , un triangolo le cui lunghezze dei lati quadrati formano una progressione aritmetica, incluso il triangolo rettangolo con le lunghezze dei lati${\displaystyle 1:{\sqrt {2}}:{\sqrt {3}}}$
• Triangolo aureo , un triangolo isoscele il cui rapporto tra la base e la lunghezza dei lati è il rapporto aureo.

Riferimenti