Funzione finestra - Window function
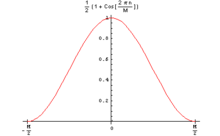
In elaborazione del segnale e statistiche , una funzione finestra (noto anche come funzione apodizzazione o funzione rastremata ) è una funzione matematica che è zero-valutati fuori di qualche prescelto intervallo , normalmente simmetrica intorno alla metà dell'intervallo, di solito in prossimità di un massimo nel medio, e di solito si assottiglia lontano dal centro. Matematicamente, quando un'altra funzione o forma d'onda/sequenza di dati viene "moltiplicata" per una funzione finestra, il prodotto viene valutato zero anche al di fuori dell'intervallo: rimane solo la parte in cui si sovrappongono, la "vista attraverso la finestra". In modo equivalente, e in pratica, il segmento di dati all'interno della finestra viene prima isolato, quindi solo quei dati vengono moltiplicati per i valori della funzione finestra. Pertanto, il tapering , non la segmentazione, è lo scopo principale delle funzioni della finestra.
Le ragioni per esaminare segmenti di una funzione più lunga includono il rilevamento di eventi transitori e la media temporale degli spettri di frequenza. La durata dei segmenti è determinata in ciascuna applicazione da requisiti come la risoluzione di tempo e frequenza. Ma quel metodo modifica anche il contenuto in frequenza del segnale mediante un effetto chiamato dispersione spettrale . Le funzioni finestra ci consentono di distribuire spettralmente la perdita in modi diversi, a seconda delle esigenze della particolare applicazione. Ci sono molte scelte dettagliate in questo articolo, ma molte delle differenze sono così sottili da essere insignificanti nella pratica.
Nelle applicazioni tipiche, le funzioni della finestra utilizzate sono curve non negative, lisce, "a campana". È possibile utilizzare anche rettangolo, triangolo e altre funzioni. Una definizione più generale di funzioni finestra non richiede che siano identicamente zero al di fuori di un intervallo, purché il prodotto della finestra moltiplicato per il suo argomento sia integrabile al quadrato e, più specificamente, che la funzione vada sufficientemente rapidamente verso lo zero.
Applicazioni
Le funzioni finestra sono utilizzate nell'analisi /modifica/ resintesi spettrale , nella progettazione di filtri a risposta impulsiva finita , nonché nel beamforming e nella progettazione di antenne .
Analisi spettrale
La trasformata di Fourier della funzione cos( ωt ) è zero, tranne che alla frequenza ± ω . Tuttavia, molte altre funzioni e forme d'onda non hanno comode trasformazioni in forma chiusa. In alternativa, si potrebbe essere interessati al loro contenuto spettrale solo durante un certo periodo di tempo.
In entrambi i casi, la trasformata di Fourier (o una trasformata simile) può essere applicata su uno o più intervalli finiti della forma d'onda. In generale, la trasformata viene applicata al prodotto della forma d'onda e una funzione finestra. Qualsiasi finestra (inclusa quella rettangolare) influisce sulla stima spettrale calcolata con questo metodo.

Scelta della funzione finestra
Il windowing di una forma d'onda semplice come cos( ωt ) fa sì che la sua trasformata di Fourier sviluppi valori diversi da zero (comunemente chiamati dispersione spettrale ) a frequenze diverse da ω . La perdita tende ad essere peggiore (massimo) vicino ω e almeno a frequenze più lontane da ω .
Se la forma d'onda in analisi comprende due sinusoidi di frequenze diverse, la perdita può interferire con la nostra capacità di distinguerle spettralmente. I possibili tipi di interferenza sono spesso suddivisi in due classi opposte come segue: se le frequenze dei componenti sono dissimili e un componente è più debole, la perdita dal componente più forte può oscurare la presenza di quello più debole. Ma se le frequenze sono troppo simili, le perdite possono renderle irrisolvibili anche quando le sinusoidi sono di uguale forza. Le finestre che sono efficaci contro il primo tipo di interferenza, ovvero dove i componenti hanno frequenze e ampiezze dissimili, sono chiamate high dynamic range . Al contrario, le finestre che possono distinguere componenti con frequenze e ampiezze simili sono chiamate ad alta risoluzione .
La finestra rettangolare è un esempio di finestra ad alta risoluzione ma bassa gamma dinamica , vale a dire che è buona per distinguere componenti di ampiezza simile anche quando le frequenze sono anche vicine, ma scarsa nel distinguere componenti di ampiezza diversa anche quando le frequenze sono lontane via. Le finestre ad alta risoluzione e a bassa gamma dinamica come la finestra rettangolare hanno anche la proprietà di un'elevata sensibilità , che è la capacità di rivelare sinusoidi relativamente deboli in presenza di rumore casuale additivo. Questo perché il rumore produce una risposta più forte con le finestre ad alta gamma dinamica rispetto alle finestre ad alta risoluzione.
All'estremo opposto della gamma di tipi di finestre ci sono le finestre con un'elevata gamma dinamica ma una bassa risoluzione e sensibilità. Le finestre ad alta gamma dinamica sono spesso giustificate nelle applicazioni a banda larga , dove si prevede che lo spettro analizzato contenga molti componenti diversi di varie ampiezze.
Tra gli estremi ci sono finestre moderate, come Hamming e Hann . Sono comunemente usati nelle applicazioni a banda stretta , come lo spettro di un canale telefonico.
In sintesi, l'analisi spettrale implica un compromesso tra la risoluzione di componenti di forza comparabili con frequenze simili ( alta risoluzione/sensibilità ) e la risoluzione di componenti di forza disparate con frequenze dissimili ( alta gamma dinamica ). Questo compromesso si verifica quando viene scelta la funzione finestra.
Segnali a tempo discreto
Quando la forma d'onda in ingresso è campionata nel tempo, anziché continua, l'analisi viene solitamente eseguita applicando una funzione finestra e quindi una trasformata discreta di Fourier (DFT). Ma la DFT fornisce solo un campionamento sparso dell'effettivo spettro della trasformata di Fourier a tempo discreto (DTFT). La Figura 2, riga 3 mostra un DTFT per una sinusoide a finestra rettangolare. La frequenza effettiva della sinusoide è indicata come "13" sull'asse orizzontale. Tutto il resto è perdita, esagerata dall'uso di una presentazione logaritmica. L'unità di frequenza è "bins DFT"; cioè, i valori interi sull'asse delle frequenze corrispondono alle frequenze campionate dal DFT. Quindi la figura rappresenta un caso in cui la frequenza effettiva della sinusoide coincide con un campione DFT e il valore massimo dello spettro viene misurato con precisione da quel campione. Nella riga 4, manca il valore massimo di ½ bin e l'errore di misurazione risultante è indicato come perdita di smerlatura (ispirata alla forma del picco). Per una frequenza nota, come una nota musicale o un segnale di prova sinusoidale, l'adattamento della frequenza a un bin DFT può essere prestabilito scegliendo una frequenza di campionamento e una lunghezza della finestra che risulta in un numero intero di cicli all'interno della finestra.
Larghezza di banda del rumore
I concetti di risoluzione e gamma dinamica tendono ad essere in qualche modo soggettivi, a seconda di ciò che l'utente sta effettivamente cercando di fare. Ma tendono anche ad essere altamente correlati con la perdita totale, che è quantificabile. Di solito è espresso come larghezza di banda equivalente, B. Può essere pensato come ridistribuire il DTFT in una forma rettangolare con altezza pari al massimo spettrale e larghezza B. Maggiore è la dispersione, maggiore è la larghezza di banda. A volte viene chiamata larghezza di banda equivalente del rumore o larghezza di banda del rumore equivalente , perché è proporzionale alla potenza media che verrà registrata da ciascun bin DFT quando il segnale di ingresso contiene un componente di rumore casuale (o è solo rumore casuale). Un grafico dello spettro di potenza , mediato nel tempo, rivela tipicamente un rumore di fondo piatto , causato da questo effetto. L'altezza del rumore di fondo è proporzionale a B. Quindi due diverse funzioni della finestra possono produrre diversi piani di rumore.
Guadagno e perdita di elaborazione
Nel trattamento del segnale , le operazioni vengono scelti per migliorare alcuni aspetti della qualità di un segnale sfruttando le differenze tra il segnale e le influenze corruttrici. Quando il segnale è una sinusoide corrotta da rumore casuale additivo, l'analisi spettrale distribuisce i componenti del segnale e del rumore in modo diverso, spesso rendendo più facile rilevare la presenza del segnale o misurare determinate caratteristiche, come l'ampiezza e la frequenza. In effetti, il rapporto segnale/rumore (SNR) viene migliorato distribuendo il rumore in modo uniforme, concentrando la maggior parte dell'energia della sinusoide intorno a una frequenza. Guadagno di elaborazione è un termine spesso utilizzato per descrivere un miglioramento del SNR. Il guadagno di elaborazione dell'analisi spettrale dipende dalla funzione finestra, sia dalla sua larghezza di banda del rumore (B) che dalla sua potenziale perdita di scalloping. Questi effetti sono parzialmente compensati, perché le finestre con la minima smerlatura hanno naturalmente le maggiori perdite.
La Figura 3 illustra gli effetti di tre diverse funzioni finestra sullo stesso set di dati, comprendente due sinusoidi di uguale forza nel rumore additivo. Le frequenze delle sinusoidi sono scelte in modo tale che una non incontri smerlatura e l'altra incontri la massima smerlatura. Entrambe le sinusoidi subiscono una minore perdita di SNR sotto la finestra di Hann che sotto la finestra Blackman – Harris . In generale (come accennato in precedenza), questo è un deterrente all'utilizzo di finestre ad alta gamma dinamica in applicazioni a bassa gamma dinamica.
Simmetria
Le formule fornite in questo articolo producono sequenze discrete, come se fosse stata "campionata" una funzione finestra continua. (Vedi un esempio nella finestra di Kaiser .) Le sequenze di finestre per l'analisi spettrale sono simmetriche o di 1 campione in corto di simmetrica (chiamate periodiche , DFT-pari o DFT-simmetriche ). Ad esempio, una vera sequenza simmetrica, con il suo massimo in un singolo punto centrale, è generata dalla funzione MATLABhann(9,'symmetric') . L'eliminazione dell'ultimo campione produce una sequenza identica a hann(8,'periodic'). Allo stesso modo, la sequenza hann(8,'symmetric')ha due punti centrali uguali.
Alcune funzioni hanno uno o due punti finali con valore zero, che non sono necessari nella maggior parte delle applicazioni. L'eliminazione di un punto finale a valore zero non ha alcun effetto sul suo DTFT (perdita spettrale). Ma la funzione progettata per campioni N + 1 o N + 2, in previsione dell'eliminazione di uno o entrambi i punti finali, ha tipicamente un lobo principale leggermente più stretto, lobi laterali leggermente più alti e una larghezza di banda del rumore leggermente più piccola.
Simmetria DFT
Il predecessore della DFT è la trasformata finita di Fourier e le funzioni finestra erano "sempre un numero dispari di punti e mostravano una simmetria uniforme rispetto all'origine". In tal caso, il DTFT è interamente a valore reale. Quando la stessa sequenza viene spostata in una finestra di dati DFT , la DTFT diventa a valori complessi, tranne che a frequenze spaziate a intervalli regolari di Quindi, quando campionati da una DFT di lunghezza (vedi sommatoria periodica ), i campioni (chiamati coefficienti DFT ) sono ancora a valore reale. Ciò è vero anche per una DFT di lunghezza della sequenza troncata DFT-simmetrica : il troncamento influisce sulla DTFT (perdita spettrale), ma di solito di una quantità trascurabile (a meno che non sia piccola, ad esempio ≤ 20 ).
Quando le finestre vengono applicate in modo moltiplicativo ai dati effettivi, la sequenza di solito manca di simmetria e la DFT generalmente non ha valori reali. Nonostante questo avvertimento, molti autori assumono di riflesso finestre simmetriche DFT. Quindi vale la pena notare che non vi è alcun vantaggio in termini di prestazioni quando applicato ai dati del dominio del tempo, che è l'applicazione consueta. Il vantaggio dei coefficienti DFT a valori reali si realizza in alcune applicazioni esoteriche in cui il windowing è ottenuto mediante convoluzione tra i coefficienti DFT e una DFT non finestrata dei dati. In queste applicazioni, sono preferite finestre DFT simmetriche (lunghezza pari o dispari) della famiglia coseno-somma , perché la maggior parte dei loro coefficienti DFT sono valutati a zero, rendendo la convoluzione molto efficiente.
- Appunti
Progettazione del filtro
Le finestre sono talvolta utilizzate nella progettazione di filtri digitali , in particolare per convertire una risposta all'impulso "ideale" di durata infinita, come una funzione sinc , in un progetto di filtro a risposta all'impulso finita (FIR). Questo è chiamato il metodo della finestra .
Statistiche e adattamento della curva
Le funzioni finestra vengono talvolta utilizzate nel campo dell'analisi statistica per restringere l'insieme di dati analizzati a un intervallo vicino a un determinato punto, con un fattore di ponderazione che riduce l'effetto dei punti più lontani dalla porzione della curva da adattare. Nel campo dell'analisi bayesiana e dell'adattamento della curva , questo viene spesso definito kernel .
Applicazioni per finestre rettangolari
Analisi dei transitori
Quando si analizza un segnale transitorio nell'analisi modale , come un impulso, una risposta allo shock, un burst sinusoidale, un burst chirp o un burst di rumore, in cui la distribuzione dell'energia rispetto al tempo è estremamente irregolare, la finestra rettangolare può essere la più appropriata. Ad esempio, quando la maggior parte dell'energia si trova all'inizio della registrazione, una finestra non rettangolare attenua la maggior parte dell'energia, degradando il rapporto segnale-rumore.
Analisi armonica
Si potrebbe voler misurare il contenuto armonico di una nota musicale da un particolare strumento o la distorsione armonica di un amplificatore a una data frequenza. Facendo nuovamente riferimento alla Figura 2 , possiamo osservare che non vi è perdita in corrispondenza di un insieme discreto di frequenze armonicamente correlate campionate dal DFT. (I null spettrali sono in realtà zero-crossing, che non possono essere mostrati su una scala logaritmica come questa.) Questa proprietà è unica per la finestra rettangolare e deve essere opportunamente configurata per la frequenza del segnale, come descritto sopra.
Un elenco di funzioni della finestra
Convenzioni :
- è una funzione a fase zero (simmetrica rispetto a ), continua per dove è un numero intero positivo (pari o dispari).
- La sequenza è simmetrica , di lunghezza
- è DFT-simmetrico , di lunghezza
- Il parametro B visualizzato su ciascun grafico spettrale è la metrica della larghezza di banda equivalente al rumore della funzione, in unità di bin DFT .
Il campionamento sparso di un DTFT (come i DFT in Fig 2) rivela solo la perdita nei bin DFT da una sinusoide la cui frequenza è anche un bin DFT intero. I lobi laterali invisibili rivelano la perdita che ci si aspetta dalle sinusoidi ad altre frequenze. Pertanto, quando si sceglie una funzione finestra, di solito è importante campionare il DTFT in modo più denso (come facciamo in questa sezione) e scegliere una finestra che sopprima i lobi laterali a un livello accettabile.
Finestra rettangolare
La finestra rettangolare (a volte nota come boxcar o finestra di Dirichlet ) è la finestra più semplice, equivalente a sostituire tutti i valori tranne N di una sequenza di dati con zeri, facendo sembrare che la forma d'onda si accenda e si spenga improvvisamente:
Altre finestre sono progettate per moderare questi cambiamenti improvvisi, il che riduce la perdita di smerlatura e migliora la gamma dinamica, come descritto sopra ( § Analisi spettrale ).
La finestra rettangolare è il 1 ° ordine B window-spline, nonche la 0 esima potenza finestra di potere-di-sinusoidale .
Finestre B- spline
Le finestre B -spline possono essere ottenute come convoluzioni k -fold della finestra rettangolare. Includono la finestra rettangolare stessa ( k = 1), la finestra § Triangolare ( k = 2) e la finestra § Parzen ( k = 4). Definizioni alternative campionano le funzioni di base B- spline normalizzate appropriate invece di convolure finestre a tempo discreto. Una funzione base B- spline di k- esimo ordine è una funzione polinomiale a tratti di grado k −1 che si ottiene per k- fold auto-convoluzione della funzione rettangolare .
Finestra triangolare
Le finestre triangolari sono date da:
dove L può essere N , N + 1 o N + 2. La prima è anche conosciuta come finestra di Bartlett o finestra di Fejér . Tutte e tre le definizioni convergono in grande N .
La finestra triangolare è la finestra B- spline di 2° ordine . La forma L = N può essere vista come la convoluzione di due finestre rettangolari di larghezza N /2. La trasformata di Fourier del risultato sono i valori quadrati della trasformata della finestra rettangolare di mezza larghezza.
Finestra Parzen
Definendo L ≜ N + 1 , la finestra Parzen, nota anche come finestra de la Vallée Poussin , è la finestra B -spline di 4° ordine data da:
Altre finestre polinomiali
Finestra di Welch
La finestra Welch è costituita da un'unica sezione parabolica :
Il polinomio quadratico di definizione raggiunge un valore zero nei campioni appena fuori dall'intervallo della finestra.
finestra sinusoidale
La corrispondente funzione è un coseno senza π / 2 spostamento di fase. Quindi la finestra del seno è talvolta chiamata anche finestra del coseno . Poiché rappresenta un mezzo ciclo di una funzione sinusoidale, è anche noto in modo variabile come finestra semiseno o semiseno .
L' autocorrelazione di una finestra sinusoidale produce una funzione nota come finestra di Bohman.
Finestre potenza di seno/coseno
Queste funzioni della finestra hanno la forma:
La finestra rettangolare ( α = 0 ), la finestra sinusoidale ( α = 1 ) e la finestra di Hann ( α = 2 ) sono membri di questa famiglia.
Per valori interi pari di α , queste funzioni possono essere espresse anche in forma coseno-somma :
Finestre coseno-somma
Questa famiglia è anche nota come finestre del coseno generalizzate .
-
( Eq.1 )
Nella maggior parte dei casi, inclusi gli esempi seguenti, tutti i coefficienti a k ≥ 0. Queste finestre hanno solo 2 K + 1 coefficienti DFT di N punti diversi da zero .
Finestre Hann e Hamming
Le consuete finestre a somma coseno per il caso K = 1 hanno la forma:
che è facilmente (e spesso) confuso con la sua versione a fase zero:
L'impostazione produce una finestra di Hann:
prende il nome da Julius von Hann e talvolta indicato come Hanning , presumibilmente a causa delle sue somiglianze linguistiche e formule con la finestra di Hamming. È anche noto come coseno rialzato , poiché la versione a fase zero è un lobo di una funzione coseno elevata.
Questa funzione è un membro di entrambe le famiglie della somma del coseno e della potenza del seno . A differenza della finestra di Hamming , i punti finali della finestra di Hann toccano lo zero. I lobi laterali risultanti escono a circa 18 dB per ottava.
L'impostazione a circa 0,54, o più precisamente 25/46, produce la finestra di Hamming, proposta da Richard W. Hamming . Tale scelta pone uno zero-crossing alla frequenza 5 π /( N − 1), che cancella il primo lobo laterale della finestra di Hann, dandogli un'altezza di circa un quinto di quella della finestra di Hann. La finestra di Hamming viene spesso chiamata blip di Hamming quando viene utilizzata per la formazione del polso .
L'approssimazione dei coefficienti a due cifre decimali abbassa sostanzialmente il livello dei lobi laterali, portandolo ad una condizione quasi equiripple. In senso equiripple, i valori ottimali per i coefficienti sono a 0 = 0,53836 e a 1 = 0,46164.
Finestra Blackman
Le finestre Blackman sono definite come:
Per convenzione comune, il termine non qualificato finestra di Blackman si riferisce alla "proposta non molto seria" di Blackman di α = 0,16 ( a 0 = 0,42, a 1 = 0,5, a 2 = 0,08), che approssima da vicino l' esatto Blackman , con a 0 = 7938/18608 0,42659, un 1 = 9240/18608 0,49656 e un 2 = 1430/18608 0,076849. Questi valori esatti posizionano degli zeri al terzo e al quarto lobo laterale, ma determinano una discontinuità ai bordi e un calo di 6 dB/ott. I coefficienti troncati non annullano anche i lobi laterali, ma hanno un decadimento migliorato di 18 dB/ott.
Finestra Nuttall, derivata prima continua
La forma continua della finestra di Nuttall e la sua prima derivata sono continue ovunque, come la funzione di Hann . Cioè, la funzione va a 0 a x = ± N /2, a differenza delle finestre Blackman–Nuttall, Blackman–Harris e Hamming. Anche la finestra di Blackman ( α = 0,16 ) è continua con derivata continua al bordo, ma la "finestra di Blackman esatta" non lo è.
Finestra Blackman–Nuttall
Finestra Blackman-Harris
Una generalizzazione della famiglia Hamming, prodotta aggiungendo funzioni sinc più spostate, volte a minimizzare i livelli dei lobi laterali
Finestra superiore piatta
Una finestra flat top è una finestra con valori parzialmente negativi che ha una perdita di smerlatura minima nel dominio della frequenza. Questa proprietà è desiderabile per la misurazione delle ampiezze delle componenti di frequenza sinusoidale. Gli svantaggi dell'ampia larghezza di banda sono la scarsa risoluzione in frequenza e l'elevata larghezza di banda del rumore .
Le finestre piatte possono essere progettate utilizzando metodi di progettazione del filtro passa-basso, oppure possono essere della solita varietà a somma coseno :
La variante Matlab ha questi coefficienti:
Sono disponibili altre varianti, come i lobi laterali che si staccano al costo di valori più alti vicino al lobo principale.
Finestre Rife-Vincent
Le finestre di Rife-Vincent sono solitamente scalate per il valore medio unitario, invece del valore di picco unitario. I valori dei coefficienti sottostanti, applicati all'Eq.1 , riflettono tale consuetudine.
Classe I, Ordine 1 ( K = 1): Funzionalmente equivalente alla finestra di Hann .
Classe I, Ordine 2 ( K = 2):
La classe I è definita riducendo al minimo l'ampiezza del lobo laterale di ordine superiore. I coefficienti per ordini fino a K=4 sono tabulati.
La classe II riduce al minimo la larghezza del lobo principale per un dato lobo laterale massimo.
La classe III è un compromesso per il quale l'ordine K = 2 assomiglia alla finestra § Blackman .
Finestre regolabili
finestra gaussiana
Anche la trasformata di Fourier di una gaussiana è una gaussiana. Dal momento che il supporto di una funzione gaussiana si estende all'infinito, deve essere troncato alle estremità della finestra, o esso stesso finestrato con un'altra finestra con estremità zero.
Poiché il log di una gaussiana produce una parabola , questa può essere utilizzata per un'interpolazione quadratica quasi esatta nella stima della frequenza .
La deviazione standard della funzione gaussiana è σ · N /2 periodi di campionamento.
Finestra gaussiana confinata
La finestra gaussiana confinata produce la più piccola larghezza di frequenza quadratica media radice possibile σ ω per una data larghezza temporale ( N + 1) σ t . Queste finestre ottimizzano i prodotti di larghezza di banda tempo-frequenza RMS. Sono calcolati come autovettori minimi di una matrice dipendente da parametri. La famiglia finestra gaussiana confinato contiene la finestra § seno e la finestra § gaussiana nei casi limite di grandi e piccoli σ t , rispettivamente.
Finestra gaussiana confinata approssimativa
Definendo L ≜ N + 1 , una finestra gaussiana confinata di ampiezza temporale L × σ t è ben approssimata da:
dove è una funzione gaussiana:
La deviazione standard della finestra approssimata è asintoticamente uguale (cioè grandi valori di N ) a L × σ t per σ t < 0,14 .
Finestra normale generalizzata
Una versione più generalizzata della finestra gaussiana è la finestra normale generalizzata. Mantenendo la notazione dalla finestra gaussiana sopra, possiamo rappresentare questa finestra come
per qualsiasi anche . A , questa è una finestra gaussiana e man mano che si avvicina a , si avvicina a una finestra rettangolare. La trasformata di Fourier di questa finestra non esiste in forma chiusa per un generale . Tuttavia, dimostra gli altri vantaggi di essere una larghezza di banda regolare e regolabile. Come la finestra § Tukey , questa finestra offre naturalmente un "flat top" per controllare l'attenuazione di ampiezza di una serie storica (sulla quale non abbiamo un controllo con finestra gaussiana). In sostanza, offre un buon compromesso (controllabile), in termini di dispersione spettrale, risoluzione in frequenza e attenuazione di ampiezza, tra la finestra gaussiana e la finestra rettangolare. Vedi anche per uno studio sulla rappresentazione tempo-frequenza di questa finestra (o funzione).
Finestra Tukey
La finestra di Tukey, nota anche come finestra coseno-coseno , può essere considerata come un lobo coseno di larghezza Nα /2 (che copre Nα /2 + 1 osservazioni) che è convoluto con una finestra rettangolare di larghezza N (1 − α /2 ) .
In α = 0 diventa rettangolare e in α = 1 diventa una finestra di Hann.
Finestra Planck-taper
La cosiddetta finestra "Planck-taper" è una funzione di rilievo che è stata ampiamente utilizzata nella teoria delle partizioni dell'unità nelle varietà . È uniforme (una funzione) ovunque, ma è esattamente zero al di fuori di una regione compatta, esattamente uno su un intervallo all'interno di quella regione e varia uniformemente e monotonamente tra quei limiti. Il suo utilizzo come funzione finestra nell'elaborazione del segnale è stato suggerito per la prima volta nel contesto dell'astronomia delle onde gravitazionali , ispirata alla distribuzione di Planck . Essa è definita come tratti funzione :
La quantità di rastremazione è controllata dal parametro ε , con valori più piccoli che danno transizioni più nitide.
Finestra DPSS o Slepian
La finestra DPSS (discreta prolate spheroidal sequence) o finestra di Slepian massimizza la concentrazione di energia nel lobo principale e viene utilizzata nell'analisi spettrale multitaper , che media il rumore nello spettro e riduce la perdita di informazioni ai bordi della finestra.
Il lobo principale termina ad un bin di frequenza dato dal parametro α .
Le finestre Kaiser di seguito sono create con una semplice approssimazione alle finestre DPSS:
Finestra Kaiser
La finestra Kaiser, o Kaiser-Bessel, è una semplice approssimazione della finestra DPSS che utilizza le funzioni di Bessel , scoperte da James Kaiser .
dove è la funzione di Bessel modificata di ordine zero del primo tipo. Il parametro variabile determina il compromesso tra la larghezza del lobo principale ei livelli del lobo laterale del pattern di dispersione spettrale. La larghezza del lobo principale, tra i null, è data da in unità di bin DFT e un valore tipico di è 3.
Finestra di Dolph-Chebyshev
Riduce al minimo la norma di Chebyshev dei lobi laterali per una data larghezza del lobo principale.
La funzione finestra di Dolph-Chebyshev a fase zero è solitamente definita in termini della sua trasformata discreta di Fourier a valori reali, :
T n ( x ) è l' n -esimo polinomio di Chebyshev del primo tipo valutato in x , che può essere calcolato utilizzando
e
è l'unica soluzione reale positiva di , dove il parametro α imposta la norma di Chebyshev dei lobi laterali a -20 α decibel.
La funzione finestra può essere calcolata da W 0 ( k ) mediante una trasformata discreta inversa di Fourier (DFT):
La versione ritardata della finestra può essere ottenuta da:
che per valori pari di N deve essere calcolato come segue:
che è una DFT inversa di
Varianti:
- A causa della condizione di equiripple, la finestra nel dominio del tempo presenta discontinuità ai bordi. Un'approssimazione che li evita, consentendo alle equiripple di scendere ai bordi, è una finestra di Taylor .
- È disponibile anche un'alternativa alla definizione DFT inversa. [1] .
Finestra ultrasferica
La finestra Ultrasferica è stata introdotta nel 1984 da Roy Streit e trova applicazione nella progettazione di array di antenne, nella progettazione di filtri non ricorsivi e nell'analisi dello spettro.
Come altre finestre regolabili, la finestra Ultrasferica ha parametri che possono essere utilizzati per controllare la sua larghezza del lobo principale della trasformata di Fourier e l'ampiezza relativa del lobo laterale. Non comune ad altre finestre, ha un parametro aggiuntivo che può essere utilizzato per impostare la velocità con cui i lobi laterali diminuiscono (o aumentano) in ampiezza.
La finestra può essere espressa nel dominio del tempo come segue:
dove è il polinomio ultrasferico di grado N, e e controlla i modelli dei lobi laterali.
Alcuni valori specifici di producono altre finestre ben note: e danno rispettivamente le finestre di Dolph-Chebyshev e Saramäki . Vedere qui per l'illustrazione delle finestre ultrasferiche con parametrizzazione variata.
Finestra esponenziale o Poisson
La finestra di Poisson, o più genericamente la finestra esponenziale, aumenta esponenzialmente verso il centro della finestra e decresce esponenzialmente nella seconda metà. Poiché la funzione esponenziale non raggiunge mai lo zero, i valori della finestra ai suoi limiti sono diversi da zero (può essere vista come la moltiplicazione di una funzione esponenziale per una finestra rettangolare). È definito da
dove τ è la costante di tempo della funzione. La funzione esponenziale decade come e ≃ 2,71828 o circa 8,69 dB per costante di tempo. Questo significa che per un decadimento mirata di D dB oltre la metà della lunghezza della finestra, la costante di tempo τ è data da
Finestre ibride
Le funzioni della finestra sono state costruite anche come combinazioni moltiplicative o additive di altre finestre.
Finestra Bartlett-Hann
Finestra di Planck–Bessel
Una finestra § Planck-taper moltiplicata per una finestra Kaiser che è definita in termini di una funzione di Bessel modificata . Questa funzione di finestra ibrida è stata introdotta per diminuire il livello di picco del lobo laterale della finestra Planck-taper pur sfruttando il suo buon decadimento asintotico. Ha due parametri sintonizzabili, ε dal Planck-taper e α dalla finestra Kaiser, quindi può essere regolato per adattarsi ai requisiti di un dato segnale.
Finestra Hann–Poisson
Una finestra di Hann moltiplicata per una finestra di Poisson , che non ha lobi laterali, nel senso che (per ) la sua trasformata di Fourier si allontana per sempre dal lobo principale. Può quindi essere utilizzato in algoritmi di arrampicata in salita come il metodo di Newton . La finestra di Hann–Poisson è definita da:
dove α è un parametro che controlla la pendenza dell'esponenziale.
Altre finestre
Finestra del polinomio adattivo generalizzato (GAP)
La finestra GAP è una famiglia di funzioni finestra regolabili basate su un'espansione polinomiale simmetrica dell'ordine . È continuo con derivata continua ovunque. Con l'appropriato insieme di coefficienti di espansione e ordine di espansione, la finestra GAP può imitare tutte le funzioni note della finestra, riproducendo accuratamente le loro proprietà spettrali.
dove è la deviazione standard della sequenza.
Inoltre, partendo da un insieme di coefficienti di espansione che imita una certa funzione di finestra nota, la finestra GAP può essere ottimizzata mediante procedure di minimizzazione per ottenere un nuovo insieme di coefficienti che migliorano una o più proprietà spettrali, come la larghezza del lobo principale, il lobo laterale attenuazione e tasso di decadimento del lobo laterale. Pertanto, è possibile sviluppare una funzione finestra GAP con proprietà spettrali progettate a seconda dell'applicazione specifica.
La finestra di Lanczos
- utilizzato nel ricampionamento di Lanczos
- per la finestra di Lanczos, è definita come
- nota anche come finestra sinc , perché :
- è il lobo principale di una funzione sinc normalizzata
Confronto di finestre
Quando si seleziona una funzione finestra appropriata per un'applicazione, questo grafico di confronto può essere utile. L'asse della frequenza ha unità di "bin" FFT quando la finestra di lunghezza N viene applicata ai dati e viene calcolata una trasformata di lunghezza N. Ad esempio, il valore alla frequenza ½ "bin" (terzo segno di graduazione) è la risposta che verrebbe misurata nei bin k e k + 1 a un segnale sinusoidale alla frequenza k + ½. È relativo alla massima risposta possibile, che si verifica quando la frequenza del segnale è un numero intero di bin. Il valore alla frequenza ½ è indicato come la massima perdita di smerlatura della finestra, che è una metrica utilizzata per confrontare le finestre. La finestra rettangolare è notevolmente peggiore delle altre in termini di quella metrica.
Altre metriche che possono essere viste sono la larghezza del lobo principale e il livello di picco dei lobi laterali, che determinano rispettivamente la capacità di risolvere segnali di forza comparabili e segnali di forza disparati. La finestra rettangolare (per esempio) è la scelta migliore per la prima e la scelta peggiore per la seconda. Ciò che non si può vedere dai grafici è che la finestra rettangolare ha la migliore larghezza di banda del rumore, il che la rende un buon candidato per rilevare sinusoidi di basso livello in un ambiente altrimenti con rumore bianco . Sono disponibili tecniche di interpolazione, come zero-padding e frequency-shifting, per mitigare la sua potenziale perdita di smerlatura.
Finestre sovrapposte
Quando la lunghezza di un set di dati da trasformare è maggiore del necessario per fornire la risoluzione di frequenza desiderata, una pratica comune è suddividerlo in insiemi più piccoli e finestrarli singolarmente. Per mitigare la "perdita" ai bordi della finestra, i singoli insiemi possono sovrapporsi nel tempo. Vedere il metodo di Welch per l'analisi spettrale di potenza e la trasformata del coseno discreta modificata .
Finestre bidimensionali
Le finestre bidimensionali sono comunemente utilizzate nell'elaborazione delle immagini per ridurre le alte frequenze indesiderate nella trasformata di Fourier dell'immagine. Possono essere costruiti da finestre unidimensionali in una delle due forme. La forma separabile, è banale da calcolare. La forma radiale , , che coinvolge il raggio , è isotropa , indipendente dall'orientamento degli assi coordinati. Solo la funzione gaussiana è sia separabile che isotropa. Le forme separabili di tutte le altre funzioni finestra hanno angoli che dipendono dalla scelta degli assi coordinati. L'isotropia/ anisotropia di una funzione finestra bidimensionale è condivisa dalla sua trasformata di Fourier bidimensionale. La differenza tra le forme separabili e radiali è simile al risultato della diffrazione da aperture rettangolari rispetto a aperture circolari, che possono essere visualizzate rispettivamente in termini di prodotto di due funzioni sinc rispetto a una funzione di Airy .
Guarda anche
- Perdita spettrale
- Multitaper
- apodizzazione
- Metodo Welch
- Trasformata di Fourier a breve termine
- Metodo di progettazione della finestra
- Filtro Kolmogorov–Zurbenko
Appunti
Citazioni della pagina
Riferimenti
Ulteriori letture
- Harris, Frederic J. (settembre 1976). "Finestre, analisi armonica e trasformata discreta di Fourier" (PDF) . apps.dtic.mil . Centro sottomarino navale, San Diego . Estratto 08-04-2019 .
- Albrecht, Hans Helge (2012). Finestre a somma del coseno del lobo laterale minimo e del lobo laterale minimo personalizzate. Versione 1.0 . ISBN 978-3-86918-281-0). editore: Physikalisch-Technische Bundesanstalt. Physikalisch-Technische Bundesanstalt. doi : 10.7795/110.20121022aa . ISBN 978-3-86918-281-0.
- Bergen, SWA; Antoniou, A. (2005). "Progettazione di filtri digitali non ricorsivi utilizzando la funzione finestra ultrasferica" . EURASIP Journal on Applied Signal Processing . 2005 (12): 1910-1922. Bibcode : 2005EJASP2005...44B . doi : 10.1155/ASP.2005.1910 .
- Prabhu, KMM (2014). Funzioni della finestra e loro applicazioni nell'elaborazione del segnale . Boca Raton, FL: CRC Press. ISBN 978-1-4665-1583-3.
- Brevetto USA 7065150 , Park, Young-Seo, "Sistema e metodo per generare una modulazione di multiplexing a divisione di frequenza ortogonale del coseno rialzato radice (RRC OFDM)", pubblicato nel 2003, pubblicato nel 2006
link esterno
-
 Media relativi alla funzione Window su Wikimedia Commons
Media relativi alla funzione Window su Wikimedia Commons - Guida di LabView, Caratteristiche dei filtri di livellamento , http://zone.ni.com/reference/en-XX/help/371361B-01/lvanlsconcepts/char_smoothing_windows/
- Creazione e proprietà delle funzioni finestra somma coseno, http://electronicsart.weebly.com/fftwindows.html
- Simulazione interattiva online di FFT, Windows, risoluzione e perdite | RITEC | Libreria e strumenti




![{\displaystyle [0\leq n\leq N],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26cc1478a6bb711340dd37b5398448eb1b8d9ef6)


![{\displaystyle [0\leq n\leq N-1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aeb6f361f87ffe5498e6b67eeb9d61976220f988)


![{\displaystyle x\in [-N/2,N/2],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0377d29e5715ebdd13819c1cc07c4638a0156afd)
![{\displaystyle \{w[n]=w_{0}(nN/2),\quad 0\leq n\leq N\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f28eb10c2426fe0deb507ce933eb6b5df2c020e)

![{\displaystyle \{w[n],\quad 0\leq n\leq N-1\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f506d61ded38a4f9d8ecd59004fbf34e793d81f3)


![{\displaystyle w[n]=1.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f071fdd6a0a02d6d9dc3c1325d88a6dda6a92781)
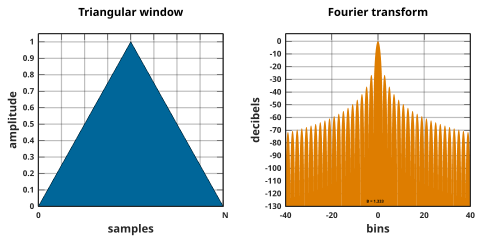
![{\displaystyle w[n]=1-\left|{\frac {n-{\frac {N}{2}}}{\frac {L}{2}}}\right|,\quad 0\leq n\leq N}](https://wikimedia.org/api/rest_v1/media/math/render/svg/884ef77423e593a74ebf40ec3eaa0c8f00ca5102)


![{\displaystyle w[n]=\ w_{0}\left(n-{\tfrac {N}{2}}\right),\ 0\leq n\leq N}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cfa5797bd28cc542de9f224e4b9c7c0c37bff91a)

![{\displaystyle w[n]=1-\left({\frac {n-{\frac {N}{2}}}{\frac {N}{2}}}\right)^{2},\ quad 0\leq n\leq N.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa3a944c6a5c2051217a53dd60a9693dd76c98a9)

![{\displaystyle w[n]=\sin \left({\frac {\pi n}{N}}\right)=\cos \left({\frac {\pi n}{N}}-{\frac {\pi }{2}}\right),\quad 0\leq n\leq N.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc2af9f7febc105f1184bd114a1484bf16cf7325)

![{\displaystyle w[n]=\sin ^{\alpha }\left({\frac {\pi n}{N}}\right)=\cos ^{\alpha }\left({\frac {\pi n}{N}}-{\frac {\pi }{2}}\right),\quad 0\leq n\leq N.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b81af4c85e4b5e6909b3dfb7fef170a42a02f7e)
![{\displaystyle w[n]=a_{0}-a_{1}\cos \left({\frac {2\pi n}{N}}\right)+a_{2}\cos \left({\ frac {4\pi n}{N}}\right)-a_{3}\cos \left({\frac {6\pi n}{N}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55aa618bd5010d83e5df4ae06fbb3abd509f12fd)

![{\displaystyle w[n]=\sum _{k=0}^{K}(-1)^{k}a_{k}\;\cos \left({\frac {2\pi kn}{N }}\right),\quad 0\leq n\leq N.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e597f0587d0c29feaf791fef475cf419be2987c9)


![{\displaystyle w[n]=a_{0}-\underbrace {(1-a_{0})} _{a_{1}}\cdot \cos \left({\tfrac {2\pi n}{N }}\right),\quad 0\leq n\leq N,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72b8f8c3192b06191db2bb7ad9247eeba6a6cb70)
![{\displaystyle {\begin{aligned}w_{0}(n)\ &=w\left[n+{\tfrac {N}{2}}\right]\\&=a_{0}+a_{1} \cdot \cos \left({\tfrac {2\pi n}{N}}\right),\quad -{\tfrac {N}{2}}\leq n\leq {\tfrac {N}{2 }}.\end{allineato}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a04d79e8c4de591b5badfd2864ebe7522c17b1ad)

![{\displaystyle w[n]=0.5\;\left[1-\cos \left({\frac {2\pi n}{N}}\right)\right]=\sin ^{2}\left( {\frac {\pi n}{N}}\right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd8d3e844a1443d7bedd57240588cf19fcd28af1)


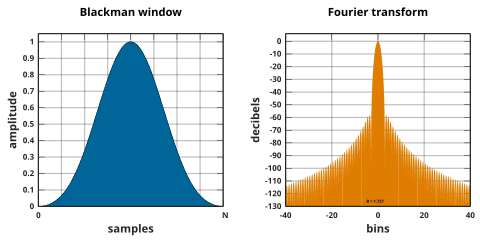
![{\displaystyle w[n]=a_{0}-a_{1}\cos \left({\frac {2\pi n}{N}}\right)+a_{2}\cos \left({\ frac {4\pi n}{N}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e1a6c47fc77da0b81229c3234068706a6ca8e6a)








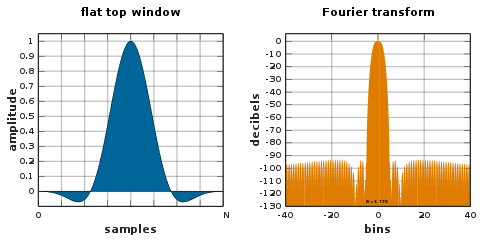
![{\displaystyle {\begin{aligned}w[n]=a_{0}&{}-a_{1}\cos \left({\frac {2\pi n}{N}}\right)+a_{ 2}\cos \left({\frac {4\pi n}{N}}\right)\\&{}-a_{3}\cos \left({\frac {6\pi n}{N} }\right)+a_{4}\cos \left({\frac {8\pi n}{N}}\right).\end{allineato}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e117d087bf8d6345fb6ea8ffc7b5aa7f6faae4a)



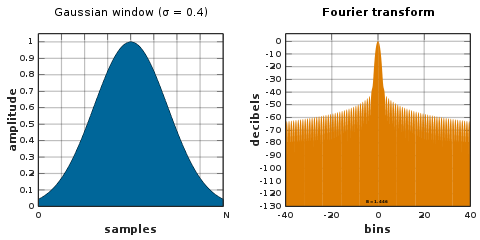
![{\displaystyle w[n]=\exp \left(-{\frac {1}{2}}\left({\frac {nN/2}{\sigma N/2}}\right)^{2} \right),\quad 0\leq n\leq N.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e201c829f6aabf4339fc0a1929367d5613dfe290)

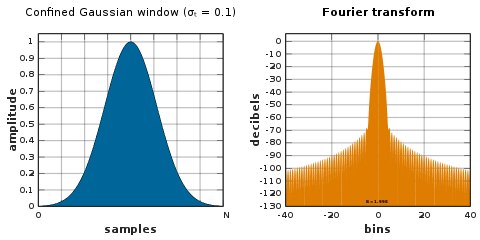

![{\displaystyle w[n]=G(n)-{\frac {G(-{\tfrac {1}{2}})[G(n+L)+G(nL)]}{G(-{ \tfrac {1}{2}}+L)+G(-{\tfrac {1}{2}}-L)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3094fa9469d1e65bfdb6a4e31cdafd037a8822ec)


![{\displaystyle w[n,p]=\exp \left(-\left({\frac {nN/2}{\sigma N/2}}\right)^{p}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/704a7de7c2a67fc8a24a140a151491bd7362698c)




![{\displaystyle \left.{\begin{array}{lll}w[n]={\frac {1}{2}}\left[1-\cos \left({\frac {2\pi n}{ \alpha N}}\right)\right],\quad &0\leq n<{\frac {\alpha N}{2}}\\w[n]=1,\quad &{\frac {\alpha N }{2}}\leq n\leq {\frac {N}{2}}\\w[Nn]=w[n],\quad &0\leq n\leq {\frac {N}{2}} \end{array}}\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab34271ac62f34c531c4d6cc0b8ffd2e9793623a)


![{\displaystyle \left.{\begin{array}{lll}w[0]=0,\\w[n]=\left(1+\exp \left({\frac {\varepsilon N}{n}) }-{\frac {\varepsilon N}{\varepsilon Nn}}\right)\right)^{-1},\quad &1\leq n<\varepsilon N\\w[n]=1,\quad & \varepsilon N\leq n\leq {\frac {N}{2}}\\w[Nn]=w[n],\quad &0\leq n\leq {\frac {N}{2}}\end {array}}\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f50bb4690593ab87a47ed71fec1945a3f95b9d0d)




![{\displaystyle w[n]={\frac {I_{0}\left(\pi \alpha {\sqrt {1-\left({\frac {2n}{N}}-1\right)^{2 }}}\right)}{I_{0}(\pi \alpha )}},\quad 0\leq n\leq N}](https://wikimedia.org/api/rest_v1/media/math/render/svg/337ca65bf1465649348a8eb22356662c4188b092)





![{\displaystyle w_{0}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0d68356ad0cc45bf520fbe5be3266aa7c431cd8)
![{\displaystyle W_{0}[k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af1b9baa4526ac8ec5f39c3cd63782248015037f)





![{\displaystyle w[n]=w_{0}\left(n-{\frac {N}{2}}\right),\quad 0\leq n\leq N,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3af173b60d19716e14882dabdec080868fa3e0ae)
![{\displaystyle {\begin{aligned}w_{0}\left(n-{\frac {N}{2}}\right)={\frac {1}{N+1}}\sum _{k= 0}^{N}W_{0}(k)\cdot e^{\frac {i2\pi k(nN/2)}{N+1}}={\frac {1}{N+1}} \sum _{k=0}^{N}\left[\left(-e^{\frac {i\pi }{N+1}}\right)^{k}\cdot W_{0}(k )\right]e^{\frac {i2\pi kn}{N+1}},\end{allineato}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24f3590133d3da32b13aa211153542e96d14a46e)


![{\displaystyle w[n]={\frac {1}{N+1}}\left[C_{N}^{\mu }(x_{0})+\sum _{k=1}^{\ frac {N}{2}}C_{N}^{\mu }\left(x_{0}\cos {\frac {k\pi }{N+1}}\right)\cos {\frac {2} \pi k}{N+1}}\destra]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe5e8dc43d2c5edbe601e3abf542a177689f4276)







![{\displaystyle w[n]=e^{-\left|n-{\frac {N}{2}}\right|{\frac {1}{\tau }}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/141d1630d759c1ebf5120671e36f86a6117f259c)

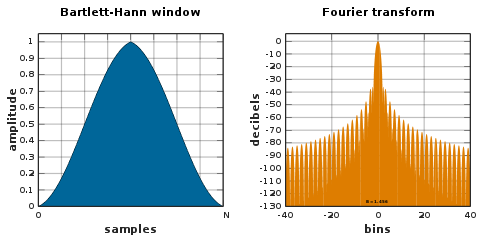
![{\displaystyle w[n]=a_{0}-a_{1}\left|{\frac {n}{N}}-{\frac {1}{2}}\right|-a_{2}\ cos \left({\frac {2\pi n}{N}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e64d33f0c717a2b40af2ed16c9fff5f58d95b937)




![{\displaystyle w[n]={\frac {1}{2}}\left(1-\cos \left({\frac {2\pi n}{N}}\right)\right)e^{ \frac {-\alpha \left|N-2n\right|}{N}}\,=\operatorname {hav} \left({\frac {2\pi n}{N}}\right)e^{ \frac {-\alpha \left|N-2n\right|}{N}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85cca45da54e9171ac868a34aeaa1311d2434e18)


![{\displaystyle w_{0}[n]=a_{0}+\sum _{k=1}^{K}a_{2k}\left({\frac {n}{\sigma }}\right)^ {2k},\quad -{\frac {N}{2}}\leq n\leq {\frac {N}{2}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0985efd235d3dcfbd7c9a2631aa173cd5c2d4cdf)




![{\displaystyle w[n]=\operatorname {sinc} \left({\frac {2n}{N}}-1\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/380ec565d5a93c55eb9d1109065556115b5c0f99)






