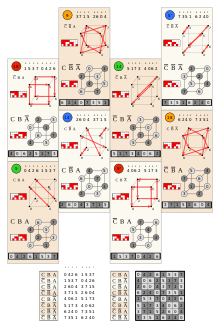
Gruppo iperottaedrico - Hyperoctahedral group

Il gruppo C 2 ha ordine 8 come mostrato in questo cerchio

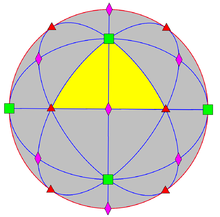
Il C 3 (O h ) gruppo ha ordine 48, come mostrato da questi domini triangolo riflessione sferiche .

In matematica , un gruppo iperottaedrico è un tipo importante di gruppo che può essere realizzato come il gruppo di simmetrie di un ipercubo o di un politopo incrociato . È stato nominato da Alfred Young nel 1930. I gruppi di questo tipo sono identificati da un parametro n , la dimensione dell'ipercubo.

Come gruppo di Coxeter è di tipo B _n = C _n , e come gruppo di Weyl è associato ai gruppi simplettici e ai gruppi ortogonali in dimensioni dispari. Come prodotto di ghirlande è dove si trova il gruppo simmetrico di grado n . Come gruppo di permutazioni , il gruppo è il gruppo simmetrico con segno di permutazioni  π o dell'insieme { − n , − n  + 1, ..., -1, 2, ..., n } o dell'insieme { − n , − n  + 1, ..., n } tale che π ( i ) = − π (− i ) per ogni  i . Come gruppo di matrici , può essere descritto come il gruppo di n × n matrici ortogonali i cui elementi sono tutti interi . La teoria della rappresentazione del gruppo iperottaedrico è stata descritta da ( Young 1930 ) secondo ( Kerber 1971 , p. 2). ${\displaystyle S_{2}\wr S_{n}}$${\displaystyle S_{n}}$

In tre dimensioni, il gruppo iperottaedrico è noto come O × S ₂ dove O ≅ S ₄ è il gruppo ottaedrico e S ₂ è un gruppo simmetrico (qui un gruppo ciclico ) di ordine 2. Figure geometriche in tre dimensioni con questo gruppo di simmetria si dice che abbiano simmetria ottaedrica , dal nome dell'ottaedro regolare , o 3- ortoplex . In 4-dimensioni è chiamata simmetria esadecacorica , dopo il normale 16-celle , o 4- ortoplex . In due dimensioni, la struttura del gruppo iperottaedrico è il gruppo diedro astratto di ordine otto , che descrive la simmetria di un quadrato , o 2-ortoplex.

Per dimensione

Le 8 permutazioni del quadrato, formando D ₄

8 delle 48 permutazioni di un cubo, formando O _h

I gruppi iperottaedrici possono essere nominati come B _n , una notazione tra parentesi o come un grafico di gruppo di Coxeter:

n	Gruppo di simmetria	B n	notazione Coxeter		Ordine	Specchi	Struttura	Politopi regolari correlati
2	RE 4 (*4•)	SI 2	[4]		2 2 2! = 8	4	${\displaystyle Dih_{4}}$ ${\displaystyle \cong S_{2}\wr S_{2}}$	Quadrato , ottagono
3	O h ( * 432 )	SI 3	[4,3]		2 3 3! = 48	3+6	${\displaystyle S_{4}\times S_{2}}$ ${\displaystyle \cong S_{2}\wr S_{3}}$	Cubo , ottaedro
4	± 1 / 6 [OxO].2 (O/V;O/V) *	SI 4	[4,3,3]		2 4 4! = 384	4+12	${\displaystyle S_{2}\wr S_{4}}$	Tesseract , 16 celle , 24 celle
5		SI 5	[4,3,3,3]		2 5 5! = 3840	5+20	${\displaystyle S_{2}\wr S_{5}}$	5-cubo , 5-ortoplex
6		SI 6	[4,3 4 ]		2 6 6! = 46080	6+30	${\displaystyle S_{2}\wr S_{6}}$	6-cubo , 6-ortoplex
...n		B n	[4,3 n-2 ]	...	2 n n ! =  ( 2n )!!	n 2	${\displaystyle S_{2}\wr S_{n}}$	ipercubo , ortoplesso

sottogruppi

Notevole è il sottogruppo indice due, corrispondente al gruppo di Coxeter D _n e alle simmetrie del demiipercubo . Viste come un prodotto della corona, ci sono due mappe naturali dal gruppo iperottaedrico al gruppo ciclico di ordine 2: una mappa proveniente da "moltiplicare i segni di tutti gli elementi" (nelle n copie di ), e una mappa proveniente dal parità di permutazione. Moltiplicandoli insieme si ottiene una terza mappa . Il nucleo della prima mappa è il gruppo di Coxeter. In termini di permutazioni con segno , pensate come matrici, questa terza mappa è semplicemente il determinante, mentre le prime due corrispondono a "moltiplicazione degli elementi diversi da zero" e "parità del sottostante ( unsigned) permutation", che non sono generalmente significative per le matrici, ma nel caso sono dovute alla coincidenza con un prodotto di ghirlande. ${\displaystyle \{\pm 1\}}$${\displaystyle C_{n}\to \{\pm 1\}}$${\displaystyle D_{n}.}$

I nuclei di queste tre mappe sono tutti e tre i sottogruppi indice due del gruppo iperottaedrico, come discusso in H ₁ : Abelianizzazione di seguito, e la loro intersezione è il sottogruppo derivato , dell'indice 4 (quoziente del gruppo 4 di Klein), che corrisponde al simmetrie rotazionali del semiipercubo.

Nell'altra direzione, il centro è il sottogruppo delle matrici scalari, {±1}; geometricamente, quoziente per questo corrisponde a passare al gruppo proiettivo ortogonale .

In dimensione 2 questi gruppi descrivono completamente il gruppo iperottaedrico, che è il gruppo diedro Dih ₄ di ordine 8 , ed è un'estensione 2.V (del gruppo 4 da un gruppo ciclico di ordine 2). In generale, passando al sottoquoziente (sottogruppo derivato, centro mod) è il gruppo di simmetria del demiipercubo proiettivo.

Simmetria tetraedrica in tre dimensioni, ordine 24

Il sottogruppo iperottaedrico , D _n per dimensione:

n	Gruppo di simmetria	D n	notazione Coxeter		Ordine	Specchi	Politopi correlati
2	RE 2 (*2•)	RE 2	[2] = [ ]×[ ]		4	2	Rettangolo
3	T d ( *332 )	RE 3	[3,3]		24	6	tetraedro
4	± 1 / 3 [Tx T ].2 (T/V;T/V) − *	RE 4	[3 1,1,1 ]		192	12	16 celle
5		RE 5	[3 2,1,1 ]		1920	20	5-semicubo
6		RE 6	[3 3,1,1 ]		23040	30	6 semicubi
...n		D n	[3 n-3,1,1 ]	...	2 n-1 n!	n(n-1)	demiipercubo

Simmetria piritoedrica in tre dimensioni, ordine 24

Simmetria ottaedrica in tre dimensioni, ordine 24

La simmetria iperottaedrica chirale , è il sottogruppo diretto, indice 2 della simmetria iperottaedrica.

n	Gruppo di simmetria	notazione Coxeter		Ordine
2	Do 4 (4•)	[4] +		4
3	O ( 432 )	[4,3] +		24
4	1 / 6 [O×O].2 (O/V;O/V)	[4,3,3] +		192
5		[4,3,3,3] +		1920
6		[4,3,3,3,3] +		23040
...n		[4,(3 n-2 ) + ]	...	2 n-1 n!

Un altro notevole sottogruppo di indice 2 può essere chiamato simmetria iperpiritoedrica , per dimensione: questi gruppi hanno n specchi ortogonali in n -dimensioni.

n	Gruppo di simmetria	notazione Coxeter		Ordine	Specchi	Politopi correlati
2	RE 2 (*2•)	[4,1 + ]=[2]		4	2	Rettangolo
3	T h ( 3*2 )	[4,3 + ]		24	3	ottaedro camuso
4	± 1 / 3 [T×T].2 (T/V;T/V) *	[4,(3,3) + ]		192	4	snobbare 24 celle
5		[4,(3,3,3) + ]		1920	5
6		[4,(3,3,3,3) + ]		23040	6
...n		[4,(3 n-2 ) + ]	...	2 n-1 n!	n

Omologia

L' omologia di gruppo del gruppo iperottaedrico è simile a quella del gruppo simmetrico e mostra stabilizzazione, nel senso della teoria dell'omotopia stabile .

H ₁ : abelianization

Il primo gruppo di omologia, che concorda con l' abelianizzazione , si stabilizza al quadrigruppo di Klein , ed è dato da:

${\displaystyle H_{1}(C_{n},\mathbf {Z} )={\begin{casi}0&n=0\\\mathbf {Z} /2&n=1\\\mathbf {Z} /2\ volte \mathbf {Z} /2&n\geq 2\end{casi}}.}$

Questo è facilmente visibile direttamente: gli elementi sono ordine 2 (che è non vuoto per ), e tutti coniugati, così come le trasposizioni in (che è non vuoto per ), e queste sono due classi separate. Questi elementi generano il gruppo, quindi le uniche abelianizzazioni non banali sono per 2-gruppi, e una di queste classi può essere inviata indipendentemente in quanto sono due classi separate. Le mappe sono date esplicitamente come "il prodotto dei segni di tutti gli elementi" (nelle n copie di ), e il segno della permutazione. Moltiplicandoli insieme si ottiene una terza mappa non banale (il determinante della matrice, che invia entrambe queste classi a ), e insieme alla mappa banale queste formano il 4-gruppo. ${\displaystyle -1}$${\displaystyle n\geq 1}$${\displaystyle S_{n}}$${\displaystyle n\geq 2}$${\displaystyle -1\in \{\pm 1\},}$${\displaystyle \{\pm 1\}}$${\displaystyle -1}$

H ₂ : Moltiplicatori Schur

I secondi gruppi di omologia, conosciuti classicamente come moltiplicatori di Schur , sono stati calcolati in ( Ihara & Yokonuma 1965 ).

Loro sono:

${\displaystyle H_{2}(C_{n},\mathbf {Z})={\begin{casi}0&n=0,1\\\mathbf {Z} /2&n=2\\(\mathbf {Z} /2)^{2}&n=3\\(\mathbf {Z} /2)^{3}&n\geq 4\end{casi}}.}$

Appunti

Riferimenti