Polytope complesso - Complex polytope
In geometria , un politopo complesso è una generalizzazione di un politopo nello spazio reale a una struttura analoga in uno spazio di Hilbert complesso , dove ogni dimensione reale è accompagnata da una dimensione immaginaria .
Un politopo complesso può essere inteso come una raccolta di punti, linee, piani e così via complessi, in cui ogni punto è la giunzione di più linee, ogni linea di più piani e così via.
Esistono definizioni precise solo per i politopi complessi regolari , che sono configurazioni . I politopi complessi regolari sono stati completamente caratterizzati e possono essere descritti utilizzando una notazione simbolica sviluppata da Coxeter .
Sono stati descritti anche alcuni politopi complessi che non sono completamente regolari.
Definizioni e introduzione
La linea complessa ha una dimensione con coordinate reali e un'altra con coordinate immaginarie . Si dice che l'applicazione di coordinate reali a entrambe le dimensioni gli dia due dimensioni rispetto ai numeri reali. Un piano reale, con l'asse immaginario etichettato come tale, è chiamato diagramma di Argand . Per questo motivo a volte viene chiamato il piano complesso. Il 2-spazio complesso (a volte chiamato anche il piano complesso) è quindi uno spazio quadridimensionale sui reali, e così via nelle dimensioni superiori.
Un n -politopo complesso nello spazio n complesso è l'analogo di un n - politopo reale nello spazio n reale .
Non esiste un analogo complesso naturale dell'ordine dei punti su una retta reale (o delle proprietà combinatorie associate). Per questo motivo un politopo complesso non può essere visto come una superficie contigua e non delimita un interno come fa un politopo reale.
Nel caso di politopi regolari , una definizione precisa può essere fatta utilizzando la nozione di simmetria. Per ogni politopo regolare il gruppo di simmetria (qui un gruppo di riflessione complesso , chiamato gruppo di Shephard ) agisce transitivamente sulle bandiere , cioè sulle sequenze annidate di un punto contenuto in una linea contenuta in un piano e così via.
Più completamente, diciamo che una raccolta P di sottospazi affini (o appartamenti ) di uno spazio unitario complesso V di dimensione n è un politopo complesso regolare se soddisfa le seguenti condizioni:
- per ogni −1 ≤ i < j < k ≤ n , se F è un appartamento in P di dimensione i e H è un appartamento in P di dimensione k tale che F ⊂ H allora ci sono almeno due appartamenti G in P di dimensione j tale che F ⊂ G ⊂ H ;
- per ogni i , j tale che −1 ≤ i < j - 2, j ≤ n , se F ⊂ G sono appartamenti di P di dimensioni i , j , allora l'insieme di appartamenti tra F e G è connesso, nel senso che si può passare da qualsiasi membro di questo insieme a qualsiasi altro mediante una sequenza di contenimenti; e
- il sottoinsieme delle trasformazioni unitarie di V che fissano P è transitivo sulle bandiere F 0 ⊂ F 1 ⊂… ⊂ F n di appartamenti di P (con F i di dimensione i per ogni i ).
(Qui, un piatto di dimensione -1 è inteso come l'insieme vuoto.) Quindi, per definizione, i politopi complessi regolari sono configurazioni nello spazio unitario complesso.
I politopi complessi regolari furono scoperti da Shephard (1952) e la teoria fu ulteriormente sviluppata da Coxeter (1974).
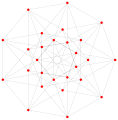
 Questo complesso poligono ha 8 bordi (linee complessi), classificati come un .. h , e 16 vertici. Quattro vertici giacciono in ogni bordo e due bordi si intersecano in ogni vertice. Nell'immagine a sinistra, i quadrati delineati non sono elementi del politopo ma sono inclusi semplicemente per aiutare a identificare i vertici che si trovano nella stessa linea complessa. Il perimetro ottagonale dell'immagine di sinistra non è un elemento del politopo, ma è un poligono pietrie . Nell'immagine centrale, ogni bordo è rappresentato come una linea reale ei quattro vertici di ciascuna linea possono essere visti più chiaramente. |
 Uno schizzo prospettico che rappresenta i 16 punti del vertice come grandi punti neri e gli 8 4 bordi come quadrati delimitati all'interno di ciascun bordo. Il percorso verde rappresenta il perimetro ottagonale dell'immagine a sinistra. |
Un politopo complesso esiste nello spazio complesso di dimensione equivalente. Ad esempio, i vertici di un poligono complesso sono punti nel piano complesso e i bordi sono linee complesse esistenti come sottospazi (affini) del piano e che si intersecano ai vertici. Pertanto, a un bordo può essere assegnato un sistema di coordinate costituito da un singolo numero complesso.
In un politopo complesso regolare i vertici incidenti sul bordo sono disposti simmetricamente rispetto al loro baricentro , che è spesso usato come origine del sistema di coordinate del bordo (nel caso reale il centroide è solo il punto medio del bordo). La simmetria nasce da una complessa riflessione sul baricentro; questa riflessione lascerà invariata la grandezza di ogni vertice, ma cambierà il suo argomento di una quantità fissa, spostandolo in ordine alle coordinate del vertice successivo. Quindi possiamo assumere (dopo un'opportuna scelta di scala) che i vertici sul bordo soddisfano l'equazione dove p è il numero di vertici incidenti. Pertanto, nel diagramma di Argand del bordo, i punti dei vertici si trovano ai vertici di un poligono regolare centrato sull'origine.
Tre proiezioni reali del poligono complesso regolare 4 {4} 2 sono illustrate sopra, con bordi a, b, c, d, e, f, g, h . Ha 16 vertici, che per chiarezza non sono stati contrassegnati individualmente. Ogni bordo ha quattro vertici e ogni vertice giace su due bordi, quindi ogni bordo incontra altri quattro bordi. Nel primo diagramma, ogni bordo è rappresentato da un quadrato. I lati del quadrato non sono parti del poligono ma sono disegnati esclusivamente per aiutare a mettere in relazione visivamente i quattro vertici. I bordi sono disposti simmetricamente. (Si noti che il diagramma è simile alla proiezione sul piano di B 4 Coxeter del tesseract , ma è strutturalmente diverso).
Il diagramma centrale abbandona la simmetria ottagonale a favore della chiarezza. Ogni bordo è mostrato come una linea reale e ogni punto di incontro di due linee è un vertice. La connettività tra i vari bordi è evidente.
L'ultimo diagramma dà un'idea della struttura proiettata in tre dimensioni: i due cubi di vertici hanno infatti le stesse dimensioni ma sono visti in prospettiva a distanze diverse nella quarta dimensione.
Polytopes unidimensionali complessi regolari

Un vero politopo monodimensionale esiste come un segmento chiuso nella linea reale , definito dai suoi due punti finali o vertici nella linea. Il suo simbolo Schläfli è {}.
Analogamente, un 1-politopo complesso esiste come un insieme di punti vertici p nella retta complessa . Questi possono essere rappresentati come un insieme di punti in un diagramma di Argand ( x , y ) = x + iy . Un politopo monodimensionale complesso regolare p {} ha p ( p ≥ 2) punti ai vertici disposti in modo da formare un poligono regolare convesso { p } nel piano di Argand.
A differenza dei punti sulla linea reale, i punti sulla linea complessa non hanno un ordine naturale. Quindi, a differenza dei veri politopi, nessun interno può essere definito. Nonostante ciò, i complessi 1-politopi sono spesso disegnati, come qui, come un poligono regolare delimitato nel piano Argand.

Un normale politopo monodimensionale reale è rappresentato da un simbolo Schläfli vuoto {}, o diagramma di Coxeter-Dynkin ![]() . Il punto o il nodo del diagramma di Coxeter-Dynkin stesso rappresenta un generatore di riflessioni mentre il cerchio attorno al nodo indica che il punto generatore non è sul riflesso, quindi la sua immagine riflettente è un punto distinto da se stessa. Per estensione, un politopo monodimensionale complesso regolare ha il diagramma di Coxeter-Dynkin
. Il punto o il nodo del diagramma di Coxeter-Dynkin stesso rappresenta un generatore di riflessioni mentre il cerchio attorno al nodo indica che il punto generatore non è sul riflesso, quindi la sua immagine riflettente è un punto distinto da se stessa. Per estensione, un politopo monodimensionale complesso regolare ha il diagramma di Coxeter-Dynkin ![]() , per qualsiasi numero intero positivo p , 2 o maggiore, contenente p vertici. p può essere soppresso se è 2. Può anche essere rappresentato da un simbolo Schläfli vuoto p {},} p {, {} p o p {2} 1 . L'1 è un segnaposto notazionale, che rappresenta una riflessione inesistente o un generatore di identità del periodo 1. (Un politopo 0, reale o complesso è un punto ed è rappresentato come} {o 1 {2} 1 ).
, per qualsiasi numero intero positivo p , 2 o maggiore, contenente p vertici. p può essere soppresso se è 2. Può anche essere rappresentato da un simbolo Schläfli vuoto p {},} p {, {} p o p {2} 1 . L'1 è un segnaposto notazionale, che rappresenta una riflessione inesistente o un generatore di identità del periodo 1. (Un politopo 0, reale o complesso è un punto ed è rappresentato come} {o 1 {2} 1 ).
La simmetria è indicata dal diagramma di Coxeter ![]() , e in alternativa può essere descritto nella notazione di Coxeter come p [], [] p o] p [, p [2] 1 o p [1] p . La simmetria è isomorfa al gruppo ciclico , ordine p . I sottogruppi di p [] sono qualsiasi divisore intero d , d [], dove d ≥2.
, e in alternativa può essere descritto nella notazione di Coxeter come p [], [] p o] p [, p [2] 1 o p [1] p . La simmetria è isomorfa al gruppo ciclico , ordine p . I sottogruppi di p [] sono qualsiasi divisore intero d , d [], dove d ≥2.
Un generatore di operatori unitari per ![]() è visto come una rotazione di 2π / p radianti in senso antiorario e a
è visto come una rotazione di 2π / p radianti in senso antiorario e a ![]() edge è creato da applicazioni sequenziali di una singola riflessione unitaria. Un generatore di riflessione unitaria per un 1-politopo con p vertici è e 2π i / p = cos (2π / p ) + i sin (2π / p ) . Quando p = 2, il generatore è e π i = –1, lo stesso di una riflessione puntuale nel piano reale.
edge è creato da applicazioni sequenziali di una singola riflessione unitaria. Un generatore di riflessione unitaria per un 1-politopo con p vertici è e 2π i / p = cos (2π / p ) + i sin (2π / p ) . Quando p = 2, il generatore è e π i = –1, lo stesso di una riflessione puntuale nel piano reale.
In politopi complessi superiori, 1-politopi formano p- bordi. Un 2-bordo è simile a un normale bordo reale, in quanto contiene due vertici, ma non è necessario che esista su una linea reale.
Poligoni complessi regolari
Mentre i politopi 1 possono avere p illimitato , i poligoni complessi regolari finiti, esclusi i poligoni a doppio prisma p {4} 2 , sono limitati a elementi a 5 bordi (bordi pentagonali) e gli apeirogoni regolari infiniti includono anche 6 bordi (bordi esagonali) elementi.
Notazioni
Notazione Schläfli modificata di Shephard
Shephard originariamente ideò una forma modificata della notazione di Schläfli per i politopi regolari. Per un poligono delimitato da p 1- bordi, con un p 2 -set come figura del vertice e gruppo di simmetria generale di ordine g , denotiamo il poligono come p 1 ( g ) p 2 .
Il numero di vertici V è quindi g / p 2 e il numero di archi E è g / p 1 .
Il poligono complesso illustrato sopra ha otto bordi quadrati ( p 1 = 4) e sedici vertici ( p 2 = 2). Da questo possiamo ricavare che g = 32, dando il simbolo Schläfli modificato 4 (32) 2.
Notazione Schläfli modificata riveduta di Coxeter
Una notazione più moderna p 1 { q } p 2 è dovuta a Coxeter e si basa sulla teoria dei gruppi. Come gruppo di simmetria, il suo simbolo è p 1 [ q ] p 2 .
Il gruppo di simmetria p 1 [ q ] p 2 è rappresentato da 2 generatori R 1 , R 2 , dove: R 1 p 1 = R 2 p 2 = I. Se q è pari, (R 2 R 1 ) q / 2 = (R 1 R 2 ) q / 2 . Se q è dispari, (R 2 R 1 ) (q-1) / 2 R 2 = (R 1 R 2 ) ( q -1) / 2 R 1 . Quando q è dispari, p 1 = p 2 .
Per 4 [4] 2 ha R 1 4 = R 2 2 = I, (R 2 R 1 ) 2 = (R 1 R 2 ) 2 .
Per 3 [5] 3 ha R 1 3 = R 2 3 = I, (R 2 R 1 ) 2 R 2 = (R 1 R 2 ) 2 R 1 .
Diagrammi di Coxeter-Dynkin
Coxeter ha anche generalizzato l'uso dei diagrammi di Coxeter-Dynkin a politopi complessi, ad esempio il poligono complesso p { q } r è rappresentato da ![]()
![]()
![]() e il gruppo di simmetria equivalente, p [ q ] r , è un diagramma senza anelli
e il gruppo di simmetria equivalente, p [ q ] r , è un diagramma senza anelli ![]()
![]()
![]() . I nodi p e r rappresentano specchi che producono immagini p e r nel piano. I nodi senza etichetta in un diagramma hanno 2 etichette implicite. Ad esempio, un poligono regolare reale è 2 { q } 2 o { q } o
. I nodi p e r rappresentano specchi che producono immagini p e r nel piano. I nodi senza etichetta in un diagramma hanno 2 etichette implicite. Ad esempio, un poligono regolare reale è 2 { q } 2 o { q } o ![]()
![]()
![]() .
.
Una limitazione, i nodi collegati da ordini di diramazione dispari devono avere ordini di nodo identici. In caso contrario, il gruppo creerà poligoni "stellati", con elementi sovrapposti. Così ![]()
![]()
![]() e
e ![]()
![]()
![]() sono normali, mentre
sono normali, mentre ![]()
![]()
![]() è stellato.
è stellato.
12 gruppi di Shephard irriducibili
Coxeter ha enumerato questo elenco di poligoni complessi regolari in formato . Un poligono complesso regolare, p { q } r o ![]()
![]()
![]() , ha p- bordi e cifre dei vertici r -gonali . p { q } r è un politopo finito se ( p + r ) q > pr ( q -2).
, ha p- bordi e cifre dei vertici r -gonali . p { q } r è un politopo finito se ( p + r ) q > pr ( q -2).
La sua simmetria è scritta come p [ q ] r , chiamato un gruppo di Shephard , analogo a un gruppo di Coxeter , pur consentendo anche riflessioni unitarie .
Per i gruppi non stellati, l'ordine del gruppo p [ q ] r può essere calcolato come .
Il numero di Coxeter per p [ q ] r è , quindi l'ordine di gruppo può anche essere calcolato come . Un poligono complesso regolare può essere disegnato in proiezione ortogonale con simmetria h -gonale.
Le soluzioni di rango 2 che generano poligoni complessi sono:
| Gruppo | G 3 = G ( q , 1,1) | G 2 = G ( p , 1,2) | G 4 | G 6 | G 5 | G 8 | G 14 | G 9 | G 10 | G 20 | G 16 | G 21 | G 17 | G 18 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 [ q ] 2 , q = 3,4 ... | p [4] 2 , p = 2,3 ... | 3 [3] 3 | 3 [6] 2 | 3 [4] 3 | 4 [3] 4 | 3 [8] 2 | 4 [6] 2 | 4 [4] 3 | 3 [5] 3 | 5 [3] 5 | 3 [10] 2 | 5 [6] 2 | 5 [4] 3 | |
|
|
||||||||||||||
| Ordine | 2 q | 2 p 2 | 24 | 48 | 72 | 96 | 144 | 192 | 288 | 360 | 600 | 720 | 1200 | 1800 |
| h | q | 2 p | 6 | 12 | 24 | 30 | 60 | |||||||
Soluzioni esclusi con dispari q e diseguale p e r sono: 6 [3] 2 , 6 [3] 3 , 9 [3] 3 , 12 [3] 3 , ..., 5 [5] 2 , 6 [5] 2 , 8 [5] 2 , 9 [5] 2 , 4 [7] 2 , 9 [5] 2 , 3 [9] 2 e 3 [11] 2 .
Altro intero q con ineguale p e r , creare gruppi stellato con sovrapposizione domini fondamentali: ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() , e
, e ![]()
![]()
![]() .
.
Il doppio poligono di p { q } r è r { q } p . Un poligono della forma p { q } p è auto-duale. I gruppi della forma p [2 q ] 2 hanno mezza simmetria p [ q ] p , quindi un poligono regolare ![]()
![]()
![]()
![]()
![]()
![]() è uguale a quasiregular
è uguale a quasiregular ![]()
![]()
![]()
![]()
![]() . Inoltre, poligono regolare con gli stessi ordini di nodi,
. Inoltre, poligono regolare con gli stessi ordini di nodi, ![]()
![]()
![]()
![]()
![]() , hanno una costruzione alternata
, hanno una costruzione alternata ![]()
![]()
![]()
![]()
![]()
![]() , consentendo ai bordi adiacenti di essere di due colori diversi.
, consentendo ai bordi adiacenti di essere di due colori diversi.
L'ordine del gruppo, g , viene utilizzato per calcolare il numero totale di vertici e bordi. Avrà vertici g / r e bordi g / p . Quando p = r , il numero di vertici e archi è uguale. Questa condizione è richiesta quando q è dispari.
Generatori di matrici
Il gruppo p [ q ] r , ![]()
![]()
![]() , può essere rappresentato da due matrici:
, può essere rappresentato da due matrici:
| Nome | R 1 |
R 2 |
|---|---|---|
| Ordine | p | r |
| Matrice |
|
|
Con
- k =
- Esempi
|
|
|
|||||||||||||||||||||||||||
|
|
|
Enumerazione di poligoni complessi regolari
Coxeter ha enumerato i poligoni complessi nella Tabella III dei Polytopes complessi regolari.
| Gruppo | Ordine | Numero di Coxeter |
Poligono | Vertici | Bordi | Appunti | ||
|---|---|---|---|---|---|---|---|---|
| G (q, q, 2) 2 [ q ] 2 = [ q ] q = 2,3,4, ... |
2 q | q | 2 { q } 2 | q | q | {} | Poligoni regolari reali Uguale a Uguale a |
|
| Gruppo | Ordine | Numero di Coxeter |
Poligono | Vertici | Bordi | Appunti | |||
|---|---|---|---|---|---|---|---|---|---|
| G ( p , 1,2) p [4] 2 p = 2,3,4, ... |
2 p 2 | 2 p | p (2 p 2 ) 2 | p {4} 2 |
|
p 2 | 2 p | p {} | uguale a p {} × p {} o rappresentazione come duoprismo p - p |
| 2 (2 p 2 ) p | 2 {4} p | 2 p | p 2 | {} | rappresentazione come duopiramide p - p | ||||
| G (2,1,2) 2 [4] 2 = [4] |
8 | 4 | 2 {4} 2 = {4} | 4 | 4 | {} | uguale a {} × {} o Piazza reale |
||
| G (3,1,2) 3 [4] 2 |
18 | 6 | 6 (18) 2 | 3 {4} 2 | 9 | 6 | 3 {} | uguale a 3 {} × 3 {} o rappresentazione come 3-3 duoprismo |
|
| 2 (18) 3 | 2 {4} 3 | 6 | 9 | {} | rappresentazione come 3-3 duopiramide | ||||
| G (4,1,2) 4 [4] 2 |
32 | 8 | 8 (32) 2 | 4 {4} 2 | 16 | 8 | 4 {} | uguale a 4 {} × 4 {} o rappresentazione come 4-4 duoprismo o {4,3,3} |
|
| 2 (32) 4 | 2 {4} 4 | 8 | 16 | {} | rappresentazione come 4-4 duopiramide o {3,3,4} | ||||
| G (5,1,2) 5 [4] 2 |
50 | 25 | 5 (50) 2 | 5 {4} 2 | 25 | 10 | 5 {} | uguale a 5 {} × 5 {} o rappresentazione come 5-5 duoprismo |
|
| 2 (50) 5 | 2 {4} 5 | 10 | 25 | {} | rappresentazione come 5-5 duopiramide | ||||
| G (6,1,2) 6 [4] 2 |
72 | 36 | 6 (72) 2 | 6 {4} 2 | 36 | 12 | 6 {} | uguale a 6 {} × 6 {} o rappresentazione come 6-6 duoprismo |
|
| 2 (72) 6 | 2 {4} 6 | 12 | 36 | {} | rappresentazione come 6-6 duopiramide | ||||
| G 4 = G (1,1,2) 3 [3] 3 <2,3,3> |
24 | 6 | 3 (24) 3 | 3 {3} 3 | 8 | 8 | 3 {} |
Configurazione Möbius – Kantor auto-duale, uguale a rappresentazione come {3,3,4} |
|
| G 6 3 [6] 2 |
48 | 12 | 3 (48) 2 | 3 {6} 2 | 24 | 16 | 3 {} | uguale a |
|
| 3 {3} 2 | poligono stellato | ||||||||
| 2 (48) 3 | 2 {6} 3 | 16 | 24 | {} | |||||
| 2 {3} 3 | poligono stellato | ||||||||
| G 5 3 [4] 3 |
72 | 12 | 3 (72) 3 | 3 {4} 3 | 24 | 24 | 3 {} | auto-duale, come rappresentazione come {3,4,3} |
|
| G 8 4 [3] 4 |
96 | 12 | 4 (96) 4 | 4 {3} 4 | 24 | 24 | 4 {} | auto-duale, come rappresentazione come {3,4,3} |
|
| G 14 3 [8] 2 |
144 | 24 | 3 (144) 2 | 3 {8} 2 | 72 | 48 | 3 {} | uguale a |
|
| 3 {8/3} 2 | poligono stellato, uguale a |
||||||||
| 2 (144) 3 | 2 {8} 3 | 48 | 72 | {} | |||||
| 2 {8/3} 3 | poligono stellato | ||||||||
| G 9 4 [6] 2 |
192 | 24 | 4 (192) 2 | 4 {6} 2 | 96 | 48 | 4 {} | uguale a |
|
| 2 (192) 4 | 2 {6} 4 | 48 | 96 | {} | |||||
| 4 {3} 2 | 96 | 48 | {} | poligono stellato | |||||
| 2 {3} 4 | 48 | 96 | {} | poligono stellato | |||||
| G 10 4 [4] 3 |
288 | 24 | 4 (288) 3 | 4 {4} 3 | 96 | 72 | 4 {} | ||
| 12 | 4 {8/3} 3 | poligono stellato | |||||||
| 24 | 3 (288) 4 | 3 {4} 4 | 72 | 96 | 3 {} | ||||
| 12 | 3 {8/3} 4 | poligono stellato | |||||||
| G 20 3 [5] 3 |
360 | 30 | 3 (360) 3 | 3 {5} 3 | 120 | 120 | 3 {} | auto-duale, come rappresentazione come {3,3,5} |
|
| 3 {5/2} 3 | auto-duplice, poligono stellato | ||||||||
| G 16 5 [3] 5 |
600 | 30 | 5 (600) 5 | 5 {3} 5 | 120 | 120 | 5 {} | auto-duale, come rappresentazione come {3,3,5} |
|
| 10 | 5 {5/2} 5 | auto-duplice, poligono stellato | |||||||
| G 21 3 [10] 2 |
720 | 60 | 3 (720) 2 | 3 {10} 2 | 360 | 240 | 3 {} | uguale a |
|
| 3 {5} 2 | poligono stellato | ||||||||
| 3 {10/3} 2 | poligono stellato, uguale a |
||||||||
| 3 {5/2} 2 | poligono stellato | ||||||||
| 2 (720) 3 | 2 {10} 3 | 240 | 360 | {} | |||||
| 2 {5} 3 | poligono stellato | ||||||||
| 2 {10/3} 3 | poligono stellato | ||||||||
| 2 {5/2} 3 | poligono stellato | ||||||||
| G 17 5 [6] 2 |
1200 | 60 | 5 (1200) 2 | 5 {6} 2 | 600 | 240 | 5 {} | uguale a |
|
| 20 | 5 {5} 2 | poligono stellato | |||||||
| 20 | 5 {10/3} 2 | poligono stellato | |||||||
| 60 | 5 {3} 2 | poligono stellato | |||||||
| 60 | 2 (1200) 5 | 2 {6} 5 | 240 | 600 | {} | ||||
| 20 | 2 {5} 5 | poligono stellato | |||||||
| 20 | 2 {10/3} 5 | poligono stellato | |||||||
| 60 | 2 {3} 5 | poligono stellato | |||||||
| G 18 5 [4] 3 |
1800 | 60 | 5 (1800) 3 | 5 {4} 3 | 600 | 360 | 5 {} | ||
| 15 | 5 {10/3} 3 | poligono stellato | |||||||
| 30 | 5 {3} 3 | poligono stellato | |||||||
| 30 | 5 {5/2} 3 | poligono stellato | |||||||
| 60 | 3 (1800) 5 | 3 {4} 5 | 360 | 600 | 3 {} | ||||
| 15 | 3 {10/3} 5 | poligono stellato | |||||||
| 30 | 3 {3} 5 | poligono stellato | |||||||
| 30 | 3 {5/2} 5 | poligono stellato | |||||||
Visualizzazioni di poligoni complessi regolari
I poligoni della forma p {2 r } q possono essere visualizzati da q set di colori di p -edge. Ciascun p -edge è visto come un poligono regolare, mentre non esistono facce.
- Proiezioni ortogonali 2D di poligoni complessi 2 { r } q
I poligoni della forma 2 {4} q sono chiamati ortoplessi generalizzati . Condividono i vertici con le duopiramidi 4D q - q , vertici collegati da 2 bordi.
- Poligoni complessi p {4} 2
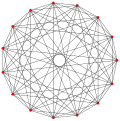
I poligoni della forma p {4} 2 sono chiamati ipercubi generalizzati (quadrati per poligoni). Condividono i vertici con i duoprismi 4D p - p , vertici collegati da archi p. Vertici sono disegnati in verde, e p -edges sono disegnati in colori alternati, rosso e blu. La prospettiva è leggermente distorta affinché le dimensioni dispari spostino i vertici sovrapposti dal centro.
- Proiezioni prospettiche 3D di poligoni complessi p {4} 2 . I doppi 2 {4} p
- si vedono aggiungendo vertici all'interno dei bordi e aggiungendo bordi al posto dei vertici.
- Altri poligoni complessi p { r } 2
- Proiezioni ortogonali 2D di poligoni complessi, p { r } p
I poligoni della forma p { r } p hanno lo stesso numero di vertici e bordi. Sono anche auto-duali.
3 {3} 3 ,


 o
o 

 , con 8 vertici in nero e 8 3 bordi colorati in 2 set di 3 bordi in rosso e blu
, con 8 vertici in nero e 8 3 bordi colorati in 2 set di 3 bordi in rosso e blu
Polytopes complessi regolari
In generale, un politopo complesso regolare è rappresentato da Coxeter come p { z 1 } q {z 2 } r {z 3 } s ... o diagramma di Coxeter ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() …, Avente simmetria p [ z 1 ] q [ z 2 ] r [ z 3 ] s … o
…, Avente simmetria p [ z 1 ] q [ z 2 ] r [ z 3 ] s … o ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ….
….
Esistono infinite famiglie di politopi complessi regolari che si verificano in tutte le dimensioni, generalizzando gli ipercubi e i politopi incrociati nello spazio reale. L '"ortotopo generalizzato" di Shephard generalizza l'ipercubo; ha il simbolo dato da γ p
n = p {4} 2 {3} 2 … 2 {3} 2 e diagramma ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ...
... ![]()
![]()
![]()
![]()
![]() . Il suo gruppo di simmetria ha il diagramma p [4] 2 [3] 2 … 2 [3] 2 ; nella classificazione Shephard-Todd, questo è il gruppo G ( p , 1, n ) che generalizza le matrici di permutazioni con segno. Il suo doppio politopo regolare, il "politopo incrociato generalizzato", è rappresentato dal simbolo β p
. Il suo gruppo di simmetria ha il diagramma p [4] 2 [3] 2 … 2 [3] 2 ; nella classificazione Shephard-Todd, questo è il gruppo G ( p , 1, n ) che generalizza le matrici di permutazioni con segno. Il suo doppio politopo regolare, il "politopo incrociato generalizzato", è rappresentato dal simbolo β p
n = 2 {3} 2 {3} 2 … 2 {4} pe diagramma ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ...
... ![]()
![]()
![]()
![]() .
.
Un politopo complesso regolare unidimensionale in è rappresentato come ![]() , avente p vertici, con la sua rappresentazione reale un poligono regolare , { p }. Coxeter gli dà anche il simbolo γ p
, avente p vertici, con la sua rappresentazione reale un poligono regolare , { p }. Coxeter gli dà anche il simbolo γ p
1 o β p
1 come ipercubo generalizzato monodimensionale o politopo incrociato. La sua simmetria è p [] o ![]() , un gruppo ciclico di ordine p . In un politopo superiore, p {} o
, un gruppo ciclico di ordine p . In un politopo superiore, p {} o ![]() rappresenta un elemento p -edge, con 2-edge, {} o
rappresenta un elemento p -edge, con 2-edge, {} o ![]() , che rappresenta un normale bordo reale tra due vertici.
, che rappresenta un normale bordo reale tra due vertici.
Un politopo complesso duale viene costruito scambiando k e ( n -1- k ) -elementi di un n -politopo. Ad esempio, un poligono doppio complesso ha vertici centrati su ciascun bordo e i nuovi bordi sono centrati sui vecchi vertici. Un vertice di v -valence crea un nuovo v -edge e gli e- edge diventano vertici di e -valence. Il duale di un politopo complesso regolare ha un simbolo invertito. Polytopes complessi regolari con simboli simmetrici, cioè p { q } p , p { q } r { q } p , p { q } r { s } r { q } p , ecc. Sono auto duali .
Enumerazione di poliedri complessi regolari
Coxeter ha enumerato questo elenco di poliedri complessi regolari non stellati in , inclusi i 5 solidi platonici in .
Un poliedro complesso regolare, p { n 1 } q { n 2 } r o ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , ha
, ha ![]()
![]()
![]()
![]()
![]()
![]() facce,
facce, ![]() bordi e
bordi e ![]()
![]()
![]()
![]()
![]()
![]() figure dei vertici .
figure dei vertici .
Un poliedro regolare complesso p { n 1 } q { n 2 } r richiede che sia g 1 = ordine ( p [ n 1 ] q ) sia g 2 = ordine ( q [ n 2 ] r ) siano finiti.
Dato g = ordine ( p [ n 1 ] q [ n 2 ] r ), il numero di vertici è g / g 2 e il numero di facce è g / g 1 . Il numero di bordi è g / pr .
| Spazio | Gruppo | Ordine | Numero di Coxeter | Poligono | Vertici | Bordi | Facce | Figura del vertice |
Poligono di Van Oss |
Appunti | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| G (1,1,3) 2 [3] 2 [3] 2 = [3,3] |
24 | 4 | α 3 = 2 {3} 2 {3} 2 = {3,3} |
4 | 6 | {} | 4 | {3} | {3} | nessuna | Tetraedro reale Uguale a |
||
| G 23 2 [3] 2 [5] 2 = [3,5] |
120 | 10 | 2 {3} 2 {5} 2 = {3,5} | 12 | 30 | {} | 20 | {3} | {5} | nessuna | Vero icosaedro | ||
| 2 {5} 2 {3} 2 = {5,3} | 20 | 30 | {} | 12 | {5} | {3} | nessuna | Dodecaedro reale | |||||
| G (2,1,3) 2 [3] 2 [4] 2 = [3,4] |
48 | 6 | β 2 3 = β 3 = {3,4} |
6 | 12 | {} | 8 | {3} | {4} | {4} | Ottaedro reale Uguale a {} + {} + {}, ordine 8 Uguale a |
||
| γ 2 3 = γ 3 = {4,3} |
8 | 12 | {} | 6 | {4} | {3} | nessuna | Cubo reale Uguale a {} × {} × {} o |
|||||
| G (p, 1,3) 2 [3] 2 [4] p p = 2,3,4, ... |
6 p 3 | 3 p | β p 3 = 2 {3} 2 {4} p |
|
3 p | 3 p 2 | {} | p 3 | {3} | 2 {4} p | 2 {4} p | Ottaedro generalizzato Uguale a p {} + p {} + p {}, ordine p 3 Uguale a |
|
| γ p 3 = p {4} 2 {3} 2 |
p 3 | 3 p 2 | p {} | 3 p | p {4} 2 | {3} | nessuna | Cubo generalizzato Uguale a p {} × p {} × p {} o |
|||||
| G (3,1,3) 2 [3] 2 [4] 3 |
162 | 9 | β 3 3 = 2 {3} 2 {4} 3 |
9 | 27 | {} | 27 | {3} | 2 {4} 3 | 2 {4} 3 | Come 3 {} + 3 {} + 3 {}, ordina 27 Come |
||
| γ 3 3 = 3 {4} 2 {3} 2 |
27 | 27 | 3 {} | 9 | 3 {4} 2 | {3} | nessuna | Uguale a 3 {} × 3 {} × 3 {} o |
|||||
| G (4,1,3) 2 [3] 2 [4] 4 |
384 | 12 | β 4 3 = 2 {3} 2 {4} 4 |
12 | 48 | {} | 64 | {3} | 2 {4} 4 | 2 {4} 4 | Uguale a 4 {} + 4 {} + 4 {}, ordina 64 Uguale a |
||
| γ 4 3 = 4 {4} 2 {3} 2 |
64 | 48 | 4 {} | 12 | 4 {4} 2 | {3} | nessuna | Uguale a 4 {} × 4 {} × 4 {} o |
|||||
| G (5,1,3) 2 [3] 2 [4] 5 |
750 | 15 | β 5 3 = 2 {3} 2 {4} 5 |
15 | 75 | {} | 125 | {3} | 2 {4} 5 | 2 {4} 5 | Uguale a 5 {} + 5 {} + 5 {}, ordina 125 Uguale a |
||
| γ 5 3 = 5 {4} 2 {3} 2 |
125 | 75 | 5 {} | 15 | 5 {4} 2 | {3} | nessuna | Uguale a 5 {} × 5 {} × 5 {} o |
|||||
| G (6,1,3) 2 [3] 2 [4] 6 |
1296 | 18 | β 6 3 = 2 {3} 2 {4} 6 |
36 | 108 | {} | 216 | {3} | 2 {4} 6 | 2 {4} 6 | Come 6 {} + 6 {} + 6 {}, ordina 216 Come |
||
| γ 6 3 = 6 {4} 2 {3} 2 |
216 | 108 | 6 {} | 18 | 6 {4} 2 | {3} | nessuna | Uguale a 6 {} × 6 {} × 6 {} o |
|||||
| G 25 3 [3] 3 [3] 3 |
648 | 9 | 3 {3} 3 {3} 3 | 27 | 72 | 3 {} | 27 | 3 {3} 3 | 3 {3} 3 | 3 {4} 2 | Uguale a |
||
| G 26 2 [4] 3 [3] 3 |
1296 | 18 | 2 {4} 3 {3} 3 | 54 | 216 | {} | 72 | 2 {4} 3 | 3 {3} 3 | {6} | |||
| 3 {3} 3 {4} 2 | 72 | 216 | 3 {} | 54 | 3 {3} 3 | 3 {4} 2 | 3 {4} 3 | Uguale a rappresentazione come 1 22 |
|||||
Visualizzazioni di poliedri complessi regolari
- Proiezioni ortogonali 2D di poliedri complessi, p { s } t { r } r
Reale {3,3} ,




 o
o 



 ha 4 vertici, 6 bordi e 4 facce
ha 4 vertici, 6 bordi e 4 facce
3 {3} 3 {3} 3 ,




 o
o 



 , ha 27 vertici, 72 3 bordi e 27 facce, con una faccia evidenziata in blu.
, ha 27 vertici, 72 3 bordi e 27 facce, con una faccia evidenziata in blu.
3 {3} 3 {4} 2 ,




 o
o 



 , ha 72 vertici, 216 a 3 lati e 54 vertici, con una faccia evidenziata in blu.
, ha 72 vertici, 216 a 3 lati e 54 vertici, con una faccia evidenziata in blu.
- Ottaedri generalizzati
Gli ottaedri generalizzati hanno una costruzione regolare come ![]()
![]()
![]()
![]()
![]() e forma quasiregolare come
e forma quasiregolare come ![]()
![]()
![]()
![]() . Tutti gli elementi sono semplici .
. Tutti gli elementi sono semplici .
Reale {3,4} ,




 o
o 

 , con 6 vertici, 12 bordi e 8 facce
, con 6 vertici, 12 bordi e 8 facce
- Cubi generalizzati
I cubi generalizzati hanno una costruzione regolare come ![]()
![]()
![]()
![]()
![]() e costruzione prismatica come
e costruzione prismatica come ![]()
![]()
![]()
![]()
![]() , un prodotto di tre 1 politopi p -gonali. Gli elementi sono cubi generalizzati di dimensione inferiore.
, un prodotto di tre 1 politopi p -gonali. Gli elementi sono cubi generalizzati di dimensione inferiore.
Reale {4,3} ,




 o
o 



 ha 8 vertici, 12 bordi e 6 facce
ha 8 vertici, 12 bordi e 6 facce
Enumerazione di 4 politopi complessi regolari
Coxeter ha enumerato questo elenco di 4-politopi complessi regolari non stellati in , inclusi i 6 4-politopi regolari convessi in .
| Spazio | Gruppo | Ordine | Numero di Coxeter |
Polytope | Vertici | Bordi | Facce | Cellule | Poligono di Van Oss |
Appunti |
|---|---|---|---|---|---|---|---|---|---|---|
| G (1,1,4) 2 [3] 2 [3] 2 [3] 2 = [3,3,3] |
120 | 5 | α 4 = 2 {3} 2 {3} 2 {3} 2 = {3,3,3} |
5 | 10 {} |
10 {3} |
5 {3,3} |
nessuna | 5 celle reali (simplex) | |
| G 28 2 [3] 2 [4] 2 [3] 2 = [3,4,3] |
1152 | 12 |
2 {3} 2 {4} 2 {3} 2 = {3,4,3} |
24 | 96 {} |
96 {3} |
24 {3,4} |
{6} | 24 celle reali | |
| G 30 2 [3] 2 [3] 2 [5] 2 = [3,3,5] |
14400 | 30 |
2 {3} 2 {3} 2 {5} 2 = {3,3,5} |
120 | 720 {} |
1200 {3} |
600 {3,3} |
{10} | 600 celle reali | |
|
2 {5} 2 {3} 2 {3} 2 = {5,3,3} |
600 | 1200 {} |
720 {5} |
120 {5,3} |
120 celle reali | |||||
| G (2,1,4) 2 [3] 2 [3] 2 [4] p = [3,3,4] |
384 | 8 | β 2 4 = β 4 = {3,3,4} |
8 | 24 {} |
32 {3} |
16 {3,3} |
{4} | 16 celle reali Come |
|
| γ 2 4 = γ 4 = {4,3,3} |
16 | 32 {} |
24 {4} |
8 {4,3} |
nessuna | Real tesseract Uguale a {} 4 o |
||||
| G (p, 1,4) 2 [3] 2 [3] 2 [4] p p = 2,3,4, ... |
24 p 4 | 4 p | β p 4 = 2 {3} 2 {3} 2 {4} p |
4 p | 6 p 2 {} |
4 p 3 {3} |
p 4 {3,3} |
2 {4} p | 4- orthoplex generalizzato Uguale a |
|
| γ p 4 = p {4} 2 {3} 2 {3} 2 |
p 4 | 4 p 3 p {} |
6 p 2 p {4} 2 |
4 p p {4} 2 {3} 2 |
nessuna | Tesseract generalizzato Uguale a p {} 4 o |
||||
| G (3,1,4) 2 [3] 2 [3] 2 [4] 3 |
1944 | 12 | β 3 4 = 2 {3} 2 {3} 2 {4} 3 |
12 | 54 {} |
108 {3} |
81 {3,3} |
2 {4} 3 | 4- orthoplex generalizzato Uguale a |
|
| γ 3 4 = 3 {4} 2 {3} 2 {3} 2 |
81 | 108 3 {} |
54 3 {4} 2 |
12 3 {4} 2 {3} 2 |
nessuna | Uguale a 3 {} 4 o |
||||
| G (4,1,4) 2 [3] 2 [3] 2 [4] 4 |
6144 | 16 | β 4 4 = 2 {3} 2 {3} 2 {4} 4 |
16 | 96 {} |
256 {3} |
64 {3,3} |
2 {4} 4 | Uguale a |
|
| γ 4 4 = 4 {4} 2 {3} 2 {3} 2 |
256 | 256 4 {} |
96 4 {4} 2 |
16 4 {4} 2 {3} 2 |
nessuna | Uguale a 4 {} 4 o |
||||
| G (5,1,4) 2 [3] 2 [3] 2 [4] 5 |
15000 | 20 | β 5 4 = 2 {3} 2 {3} 2 {4} 5 |
20 | 150 {} |
500 {3} |
625 {3,3} |
2 {4} 5 | Uguale a |
|
| γ 5 4 = 5 {4} 2 {3} 2 {3} 2 |
625 | 500 5 {} |
150 5 {4} 2 |
20 5 {4} 2 {3} 2 |
nessuna | Uguale a 5 {} 4 o |
||||
| G (6,1,4) 2 [3] 2 [3] 2 [4] 6 |
31104 | 24 | β 6 4 = 2 {3} 2 {3} 2 {4} 6 |
24 | 216 {} |
864 {3} |
1296 {3,3} |
2 {4} 6 | Uguale a |
|
| γ 6 4 = 6 {4} 2 {3} 2 {3} 2 |
1296 | 864 6 {} |
216 6 {4} 2 |
24 6 {4} 2 {3} 2 |
nessuna | Uguale a 6 {} 4 o |
||||
| G 32 3 [3] 3 [3] 3 [3] 3 |
155520 | 30 |
3 {3} 3 {3} 3 {3} 3 |
240 | 2160 3 {} |
2160 3 {3} 3 |
240 3 {3} 3 {3} 3 |
3 {4} 3 |
Witting polytope rappresentazione come 4 21 |
Visualizzazioni di 4 politopi complessi regolari
Reale {3,3,3} ,






 , aveva 5 vertici, 10 bordi, 10 {3} facce e 5 {3,3} celle
, aveva 5 vertici, 10 bordi, 10 {3} facce e 5 {3,3} celle
Reale {3,4,3} ,






 , aveva 24 vertici, 96 bordi, 96 {3} facce e 24 {3,4} celle
, aveva 24 vertici, 96 bordi, 96 {3} facce e 24 {3,4} celle
Reale {5,3,3} ,






 , aveva 600 vertici, 1200 bordi, 720 {5} facce e 120 {5,3} celle
, aveva 600 vertici, 1200 bordi, 720 {5} facce e 120 {5,3} celle
Reale {3,3,5} ,






 , aveva 120 vertici, 720 bordi, 1200 {3} facce e 600 {3,3} celle
, aveva 120 vertici, 720 bordi, 1200 {3} facce e 600 {3,3} celle
Witting polytope ,






 , ha 240 vertici, 2160 3 lati, 2160 3 {3} 3 facce e 240 3 {3} 3 {3} 3 celle
, ha 240 vertici, 2160 3 lati, 2160 3 {3} 3 facce e 240 3 {3} 3 {3} 3 celle
- 4-ortoplessi generalizzati
I 4-orthoplex generalizzati hanno una costruzione regolare come ![]()
![]()
![]()
![]()
![]()
![]()
![]() e forma quasiregolare come
e forma quasiregolare come ![]()
![]()
![]()
![]()
![]()
![]() . Tutti gli elementi sono semplici .
. Tutti gli elementi sono semplici .
Reale {3,3,4} ,






 o
o 



 , con 8 vertici, 24 bordi, 32 facce e 16 celle
, con 8 vertici, 24 bordi, 32 facce e 16 celle
- 4 cubi generalizzati
I tesseratti generalizzati hanno una costruzione regolare come ![]()
![]()
![]()
![]()
![]()
![]()
![]() e costruzione prismatica come
e costruzione prismatica come ![]()
![]()
![]()
![]()
![]()
![]()
![]() , un prodotto di quattro 1 politopi p -gonali. Gli elementi sono cubi generalizzati di dimensione inferiore.
, un prodotto di quattro 1 politopi p -gonali. Gli elementi sono cubi generalizzati di dimensione inferiore.
Reale {4,3,3} ,






 o
o 





 , con 16 vertici, 32 bordi, 24 facce e 8 celle
, con 16 vertici, 32 bordi, 24 facce e 8 celle
Enumerazione di 5 politopi complessi regolari
I 5 politopi complessi regolari in o superiori esistono in tre famiglie, i simplex reali e l' ipercubo generalizzato e l' ortoplessia .
| Spazio | Gruppo | Ordine | Polytope | Vertici | Bordi | Facce | Cellule | 4 facce | Poligono di Van Oss |
Appunti |
|---|---|---|---|---|---|---|---|---|---|---|
| G (1,1,5) = [3,3,3,3] |
720 | α 5 = {3,3,3,3} |
6 | 15 {} |
20 {3} |
15 {3,3} |
6 {3,3,3} |
nessuna | 5-simplex reale | |
| G (2,1,5) = [3,3,3,4] |
3840 | β 2 5 = β 5 = {3,3,3,4} |
10 | 40 {} |
80 {3} |
80 {3,3} |
32 {3,3,3} |
{4} | 5-orthoplex reale Uguale a |
|
| γ 2 5 = γ 5 = {4,3,3,3} |
32 | 80 {} |
80 {4} |
40 {4,3} |
10 {4,3,3} |
nessuna | 5 cubi reali Uguale a {} 5 o |
|||
| G (p, 1,5) 2 [3] 2 [3] 2 [3] 2 [4] p |
120 p 5 | β p 5 = 2 {3} 2 {3} 2 {3} 2 {4} p |
5 p | 10 p 2 {} |
10 p 3 {3} |
5 p 4 {3,3} |
p 5 {3,3,3} |
2 {4} p | 5-orthoplex generalizzato Uguale a |
|
| γ p 5 = p {4} 2 {3} 2 {3} 2 {3} 2 |
p 5 | 5 p 4 p {} |
10 p 3 p {4} 2 |
10 p 2 p {4} 2 {3} 2 |
5 p p {4} 2 {3} 2 {3} 2 |
nessuna | 5 cubi generalizzati Uguale a p {} 5 o |
|||
| G (3,1,5) 2 [3] 2 [3] 2 [3] 2 [4] 3 |
29160 | β 3 5 = 2 {3} 2 {3} 2 {3} 2 {4} 3 |
15 | 90 {} |
270 {3} |
405 {3,3} |
243 {3,3,3} |
2 {4} 3 | Uguale a |
|
| γ 3 5 = 3 {4} 2 {3} 2 {3} 2 {3} 2 |
243 | 405 3 {} |
270 3 {4} 2 |
90 3 {4} 2 {3} 2 |
15 3 {4} 2 {3} 2 {3} 2 |
nessuna | Uguale a 3 {} 5 o |
|||
| G (4,1,5) 2 [3] 2 [3] 2 [3] 2 [4] 4 |
122880 | β 4 5 = 2 {3} 2 {3} 2 {3} 2 {4} 4 |
20 | 160 {} |
640 {3} |
1280 {3,3} |
1024 {3,3,3} |
2 {4} 4 | Uguale a |
|
| γ 4 5 = 4 {4} 2 {3} 2 {3} 2 {3} 2 |
1024 | 1280 4 {} |
640 4 {4} 2 |
160 4 {4} 2 {3} 2 |
20 4 {4} 2 {3} 2 {3} 2 |
nessuna | Uguale a 4 {} 5 o |
|||
| G (5,1,5) 2 [3] 2 [3] 2 [3] 2 [4] 5 |
375000 | β 5 5 = 2 {3} 2 {3} 2 {3} 2 {5} 5 |
25 | 250 {} |
1250 {3} |
3125 {3,3} |
3125 {3,3,3} |
2 {5} 5 | Uguale a |
|
| γ 5 5 = 5 {4} 2 {3} 2 {3} 2 {3} 2 |
3125 | 3125 5 {} |
1250 5 {5} 2 |
250 5 {5} 2 {3} 2 |
25 5 {4} 2 {3} 2 {3} 2 |
nessuna | Uguale a 5 {} 5 o |
|||
| G (6,1,5) 2 [3] 2 [3] 2 [3] 2 [4] 6 |
933210 | β 6 5 = 2 {3} 2 {3} 2 {3} 2 {4} 6 |
30 | 360 {} |
2160 {3} |
6480 {3,3} |
7776 {3,3,3} |
2 {4} 6 | Uguale a |
|
| γ 6 5 = 6 {4} 2 {3} 2 {3} 2 {3} 2 |
7776 | 6480 6 {} |
2160 6 {4} 2 |
360 6 {4} 2 {3} 2 |
30 6 {4} 2 {3} 2 {3} 2 |
nessuna | Uguale a 6 {} 5 o |
Visualizzazioni di 5 politopi complessi regolari
- 5-ortoplessi generalizzati
I 5-orthoplex generalizzati hanno una costruzione regolare come ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() e forma quasiregolare come
e forma quasiregolare come ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() . Tutti gli elementi sono semplici .
. Tutti gli elementi sono semplici .
Reale {3,3,3,4} ,








 , con 10 vertici, 40 bordi, 80 facce, 80 celle e 32 4 facce
, con 10 vertici, 40 bordi, 80 facce, 80 celle e 32 4 facce
- 5 cubi generalizzati
I 5 cubi generalizzati hanno una costruzione regolare come ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() e costruzione prismatica come
e costruzione prismatica come ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , un prodotto di cinque 1 politopi p -gonali. Gli elementi sono cubi generalizzati di dimensione inferiore.
, un prodotto di cinque 1 politopi p -gonali. Gli elementi sono cubi generalizzati di dimensione inferiore.
Reale {4,3,3,3} ,








 , con 32 vertici, 80 bordi, 80 facce, 40 celle e 10 4 facce
, con 32 vertici, 80 bordi, 80 facce, 40 celle e 10 4 facce
Enumerazione di 6 politopi complessi regolari
| Spazio | Gruppo | Ordine | Polytope | Vertici | Bordi | Facce | Cellule | 4 facce | 5 facce | Poligono di Van Oss |
Appunti |
|---|---|---|---|---|---|---|---|---|---|---|---|
| G (1,1,6) = [3,3,3,3,3] |
720 | α 6 = {3,3,3,3,3} |
7 | 21 {} |
35 {3} |
35 {3,3} |
21 {3,3,3} |
7 {3,3,3,3} |
nessuna | Reale 6-simplex | |
| G (2,1,6) [3,3,3,4] |
46080 | β 2 6 = β 6 = {3,3,3,4} |
12 | 60 {} |
160 {3} |
240 {3,3} |
192 {3,3,3} |
64 {3,3,3,3} |
{4} | 6-orthoplex reale Uguale a |
|
| γ 2 6 = γ 6 = {4,3,3,3} |
64 | 192 {} |
240 {4} |
160 {4,3} |
60 {4,3,3} |
12 {4,3,3,3} |
nessuna | 6 cubi reali Uguale a {} 6 o |
|||
| G (p, 1,6) 2 [3] 2 [3] 2 [3] 2 [4] p |
720 p 6 | β p 6 = 2 {3} 2 {3} 2 {3} 2 {4} p |
6 p | 15 p 2 {} |
20 p 3 {3} |
15 p 4 {3,3} |
6 p 5 {3,3,3} |
p 6 {3,3,3,3} |
2 {4} p | 6-orthoplex generalizzato Uguale a |
|
| γ p 6 = p {4} 2 {3} 2 {3} 2 {3} 2 |
p 6 | 6 p 5 p {} |
15 p 4 p {4} 2 |
20 p 3 p {4} 2 {3} 2 |
15 p 2 p {4} 2 {3} 2 {3} 2 |
6 p p {4} 2 {3} 2 {3} 2 {3} 2 |
nessuna | 6 cubi generalizzati Uguale a p {} 6 o |
Visualizzazioni di 6 politopi complessi regolari
- 6-ortoplessi generalizzati
I 6-orthoplex generalizzati hanno una costruzione regolare come ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() e forma quasiregolare come
e forma quasiregolare come ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() . Tutti gli elementi sono semplici .
. Tutti gli elementi sono semplici .
Reale {3,3,3,3,4} ,










 , con 12 vertici, 60 bordi, 160 facce, 240 celle, 192 4 facce e 64 5 facce
, con 12 vertici, 60 bordi, 160 facce, 240 celle, 192 4 facce e 64 5 facce
- 6 cubi generalizzati
I 6 cubi generalizzati hanno una costruzione regolare come ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() e costruzione prismatica come
e costruzione prismatica come ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , un prodotto di sei 1 politopi p -gonali. Gli elementi sono cubi generalizzati di dimensione inferiore.
, un prodotto di sei 1 politopi p -gonali. Gli elementi sono cubi generalizzati di dimensione inferiore.
Reale {3,3,3,3,3,4} ,










 , con 64 vertici, 192 bordi, 240 facce, 160 celle, 60 4 facce e 12 5 facce
, con 64 vertici, 192 bordi, 240 facce, 160 celle, 60 4 facce e 12 5 facce
Enumerazione di apeirotopi complessi regolari
Coxeter ha enumerato questo elenco di apeirotopi complessi regolari non stellati o favi.
Per ogni dimensione ci sono 12 apeirotopi simboleggiati come δ p , r
n + 1 esiste in qualsiasi dimensione , o se p = q = 2. Coxeter chiama questi favi cubici generalizzati per n > 2.
Ognuno ha un conteggio proporzionale degli elementi dato come:
- k-facce = , dove e n ! indica il fattoriale di n .
1-politopi complessi regolari
L'unico politopo complesso regolare è ∞ {}, o ![]() . La sua rappresentazione reale è un apeirogon , {∞} o
. La sua rappresentazione reale è un apeirogon , {∞} o ![]()
![]()
![]() .
.
Apeirogons complessi regolari
Gli apeirogoni complessi di rango 2 hanno simmetria p [ q ] r , dove 1 / p + 2 / q + 1 / r = 1. Coxeter li esprime come δ p , r
2 dove q è vincolato a soddisfare q = 2 / (1 - ( p + r ) / pr ) .
Ci sono 8 soluzioni:
| 2 [∞] 2 | 3 [12] 2 | 4 [8] 2 | 6 [6] 2 | 3 [6] 3 | 6 [4] 3 | 4 [4] 4 | 6 [3] 6 |
|
|
Ci sono due soluzioni esclusi dispari q e diseguale p e r : 10 [5] 2 e 12 [3] 4 , o ![]()
![]()
![]() e
e ![]()
![]()
![]() .
.
Un apeirogon complesso regolare p { q } r ha p- bordi e figure dei vertici r -gonali. Il doppio apeirogon di p { q } r è r { q } p . Un apeirogon della forma p { q } p è auto-duale. I gruppi della forma p [2 q ] 2 hanno mezza simmetria p [ q ] p , quindi un apeirogon regolare ![]()
![]()
![]()
![]() è uguale a quasiregular
è uguale a quasiregular ![]()
![]()
![]() .
.
Apeirogons possono essere rappresentati sul piano Argand condividono quattro diverse disposizioni dei vertici. Apeirogons della forma 2 { q } r hanno una disposizione dei vertici come { q / 2, p }. La forma p { q } 2 ha disposizione dei vertici come r { p , q / 2}. Apeirogons della forma p {4} r hanno disposizioni dei vertici { p , r }.
Compresi i nodi affini e , ci sono altre 3 soluzioni infinite: ∞ [2] ∞ , ∞ [4] 2 , ∞ [3] 3 e ![]()
![]()
![]() ,
, ![]()
![]()
![]() , e
, e ![]()
![]()
![]() . Il primo è un sottogruppo indice 2 del secondo. I vertici di questi apeirogons esistono in .
. Il primo è un sottogruppo indice 2 del secondo. I vertici di questi apeirogons esistono in .
| Spazio | Gruppo | Apeirogon | Bordo | rappresentante. | Immagine | Appunti | |
|---|---|---|---|---|---|---|---|
| 2 [∞] 2 = [∞] | δ 2,2 2 = {∞} |
|
{} | Apeirogon reale Uguale a |
|||
| / | ∞ [4] 2 | ∞ {4} 2 | ∞ {} | {4,4} |  |
Uguale a 
|
|
| ∞ [3] 3 | ∞ {3} 3 | ∞ {} | {3,6} | Uguale a |
|||
| p [ q ] r | δ p, r 2 = p { q } r |
p {} | |||||
| 3 [12] 2 | δ 3,2 2 = 3 {12} 2 |
3 {} | r {3,6} |  |
Uguale a 
|
||
| δ 2,3 2 = 2 {12} 3 |
{} | {6,3} |  |
||||
| 3 [6] 3 | δ 3,3 2 = 3 {6} 3 |
3 {} | {3,6} | Uguale a |
|||
| 4 [8] 2 | δ 4,2 2 = 4 {8} 2 |
4 {} | {4,4} |  |
Uguale a 
|
||
| δ 2,4 2 = 2 {8} 4 |
{} | {4,4} |  |
||||
| 4 [4] 4 | δ 4,4 2 = 4 {4} 4 |
4 {} | {4,4} |  |
Uguale a |
||
| 6 [6] 2 | δ 6,2 2 = 6 {6} 2 |
6 {} | r {3,6} | Uguale a |
|||
| δ 2,6 2 = 2 {6} 6 |
{} | {3,6} | |||||
| 6 [4] 3 | δ 6,3 2 = 6 {4} 3 |
6 {} | {6,3} |  |
|||
| δ 3,6 2 = 3 {4} 6 |
3 {} | {3,6} | |||||
| 6 [3] 6 | δ 6,6 2 = 6 {3} 6 |
6 {} | {3,6} |  |
Uguale a |
||
Apeirohedra complesso regolare
Esistono 22 apeiroedri complessi regolari, della forma p { a } q { b } r . 8 sono auto-duale ( p = r ed un = b ), mentre il 14 esistono come coppie duali politopo. Tre sono completamente reali ( p = q = r = 2).
Coxeter simboleggia 12 di loro come δ p , r
3 oppure p {4} 2 {4} r è la forma regolare del prodotto apeirotopo δ p , r
2 × δ p , r
2 o p { q } r × p { q } r , dove q è determinato dal p e r .
![]()
![]()
![]()
![]()
![]() equivale a
equivale a ![]()
![]()
![]()
![]() , così come
, così come ![]()
![]()
![]()
![]()
![]()
![]()
![]() , per p , r = 2,3,4,6. Anche
, per p , r = 2,3,4,6. Anche ![]()
![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
![]() .
.
| Spazio | Gruppo | Apeirohedron | Vertice | Bordo | Viso | van Oss apeirogon |
Appunti | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 2 [3] 2 [4] ∞ | ∞ {4} 2 {3} 2 | ∞ {} | ∞ {4} 2 | Uguale a ∞ {} × ∞ {} × ∞ {} o Rappresentanza reale {4,3,4} |
||||||
| p [4] 2 [4] r | p {4} 2 {4} r |
|
p 2 | 2 pq | p {} | r 2 | p {4} 2 | 2 { q } r | Uguale a |
|
| [4,4] | δ 2,2 3 = {4,4} |
4 | 8 | {} | 4 | {4} | {∞} | Piastrellatura quadrata reale Uguale a |
||
|
3 [4] 2 [4] 2 3 [4] 2 [4] 3 4 [4] 2 [4] 2 4 [4] 2 [4] 4 6 [4] 2 [4] 2 6 [4] 2 [4] 3 6 [4] 2 [4] 6 |
3 {4} 2 {4} 2 2 {4} 2 {4} 3 3 {4} 2 {4} 3 4 {4} 2 {4} 2 2 {4} 2 {4} 4 4 {4} 2 {4} 4 6 {4} 2 {4} 2 2 {4} 2 {4} 6 6 {4} 2 {4} 3 3 {4} 2 {4} 6 6 {4} 2 {4} 6 |
|
9 4 9 16 4 16 36 4 36 9 36 |
12 12 18 16 16 32 24 24 36 36 72 |
3 {} {} 3 {} 4 {} {} 4 {} 6 {} {} 6 {} 3 {} 6 {} |
4 9 9 4 16 16 4 36 9 36 36 |
3 {4} 2 {4} 3 {4} 2 4 {4} 2 {4} 4 {4} 2 6 {4} 2 {4} 6 {4} 2 3 {4} 2 6 {4} 2 |
p { q } r | Uguale a Uguale a Uguale a Uguale a Uguale a Uguale a Uguale a Uguale a Uguale a Uguale a Uguale a |
|
| Spazio | Gruppo | Apeirohedron | Vertice | Bordo | Viso | van Oss apeirogon |
Appunti | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 2 [4] r [4] 2 | 2 {4} r {4} 2 |
|
2 | {} | 2 | p {4} 2 ' | 2 {4} r | Uguale a |
||
| [4,4] | {4,4} | 2 | 4 | {} | 2 | {4} | {∞} | Uguale a |
||
|
2 [4] 3 [4] 2 2 [4] 4 [4] 2 2 [4] 6 [4] 2 |
2 {4} 3 {4} 2 2 {4} 4 {4} 2 2 {4} 6 {4} 2 |
|
2 | 9 16 36 |
{} | 2 |
2 {4} 3 2 {4} 4 2 {4} 6 |
2 { q } r | Uguale a Uguale a Uguale a |
|
| Spazio | Gruppo | Apeirohedron | Vertice | Bordo | Viso | van Oss apeirogon |
Appunti | |||
|---|---|---|---|---|---|---|---|---|---|---|
|
2 [6] 2 [3] 2 = [6,3] |
{3,6} |
|
1 | 3 | {} | 2 | {3} | {∞} | Piastrellatura triangolare reale | |
| {6,3} | 2 | 3 | {} | 1 | {6} | nessuna | Piastrelle esagonali reali | |||
| 3 [4] 3 [3] 3 | 3 {3} 3 {4} 3 | 1 | 8 | 3 {} | 3 | 3 {3} 3 | 3 {4} 6 | Uguale a |
||
| 3 {4} 3 {3} 3 | 3 | 8 | 3 {} | 2 | 3 {4} 3 | 3 {12} 2 | ||||
| 4 [3] 4 [3] 4 | 4 {3} 4 {3} 4 | 1 | 6 | 4 {} | 1 | 4 {3} 4 | 4 {4} 4 | Auto-duale, come |
||
| 4 [3] 4 [4] 2 | 4 {3} 4 {4} 2 | 1 | 12 | 4 {} | 3 | 4 {3} 4 | 2 {8} 4 | Uguale a |
||
| 2 {4} 4 {3} 4 | 3 | 12 | {} | 1 | 2 {4} 4 | 4 {4} 4 | ||||
3-apeirotopi complessi regolari
Ci sono 16 apeirotopi complessi regolari in formato . Coxeter esprime 12 di loro con δ p , r
3 dove q è vincolato a soddisfare q = 2 / (1 - ( p + r ) / pr ) . Questi possono anche essere decomposti come apeirotopi del prodotto: ![]()
![]()
![]()
![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() . Il primo caso è il nido d'ape cubico .
. Il primo caso è il nido d'ape cubico .
| Spazio | Gruppo | 3-apeirotopo | Vertice | Bordo | Viso | Cellula | van Oss apeirogon |
Appunti |
|---|---|---|---|---|---|---|---|---|
| p [4] 2 [3] 2 [4] r | δ p , r 3 = p {4} 2 {3} 2 {4} r |
p {} | p {4} 2 | p {4} 2 {3} 2 | p { q } r | Uguale a |
||
|
2 [4] 2 [3] 2 [4] 2 = [4,3,4] |
δ 2,2 3 = 2 {4} 2 {3} 2 {4} 2 |
{} | {4} | {4,3} |
Nido d'ape cubico Uguale a |
|||
| 3 [4] 2 [3] 2 [4] 2 | δ 3,2 3 = 3 {4} 2 {3} 2 {4} 2 |
3 {} | 3 {4} 2 | 3 {4} 2 {3} 2 | Uguale a |
|||
| δ 2,3 3 = 2 {4} 2 {3} 2 {4} 3 |
{} | {4} | {4,3} | Uguale a |
||||
| 3 [4] 2 [3] 2 [4] 3 | δ 3,3 3 = 3 {4} 2 {3} 2 {4} 3 |
3 {} | 3 {4} 2 | 3 {4} 2 {3} 2 | Uguale a |
|||
| 4 [4] 2 [3] 2 [4] 2 | δ 4,2 3 = 4 {4} 2 {3} 2 {4} 2 |
4 {} | 4 {4} 2 | 4 {4} 2 {3} 2 | Uguale a |
|||
| δ 2,4 3 = 2 {4} 2 {3} 2 {4} 4 |
{} | {4} | {4,3} | Uguale a |
||||
| 4 [4] 2 [3] 2 [4] 4 | δ 4,4 3 = 4 {4} 2 {3} 2 {4} 4 |
4 {} | 4 {4} 2 | 4 {4} 2 {3} 2 | Uguale a |
|||
| 6 [4] 2 [3] 2 [4] 2 | δ 6,2 3 = 6 {4} 2 {3} 2 {4} 2 |
6 {} | 6 {4} 2 | 6 {4} 2 {3} 2 | Uguale a |
|||
| δ 2,6 3 = 2 {4} 2 {3} 2 {4} 6 |
{} | {4} | {4,3} | Uguale a |
||||
| 6 [4] 2 [3] 2 [4] 3 | δ 6,3 3 = 6 {4} 2 {3} 2 {4} 3 |
6 {} | 6 {4} 2 | 6 {4} 2 {3} 2 | Uguale a |
|||
| δ 3,6 3 = 3 {4} 2 {3} 2 {4} 6 |
3 {} | 3 {4} 2 | 3 {4} 2 {3} 2 | Uguale a |
||||
| 6 [4] 2 [3] 2 [4] 6 | δ 6,6 3 = 6 {4} 2 {3} 2 {4} 6 |
6 {} | 6 {4} 2 | 6 {4} 2 {3} 2 | Uguale a |
| Spazio | Gruppo | 3-apeirotopo | Vertice | Bordo | Viso | Cellula | van Oss apeirogon |
Appunti |
|---|---|---|---|---|---|---|---|---|
| 2 [4] 3 [3] 3 [3] 3 |
3 {3} 3 {3} 3 {4} 2 |
1 | 24 3 {} | 27 3 {3} 3 | 2 3 {3} 3 {3} 3 | 3 {4} 6 | Uguale a |
|
|
2 {4} 3 {3} 3 {3} 3 |
2 | 27 {} | 24 2 {4} 3 | 1 2 {4} 3 {3} 3 | 2 {12} 3 | |||
| 2 [3] 2 [4] 3 [3] 3 |
2 {3} 2 {4} 3 {3} 3 |
1 | 27 {} | 72 2 {3} 2 | 8 2 {3} 2 {4} 3 | 2 {6} 6 | ||
|
3 {3} 3 {4} 2 {3} 2 |
8 | 72 3 {} | 27 3 {3} 3 | 1 3 {3} 3 {4} 2 | 3 {6} 3 | Uguale a |
4-apeirotopi complessi regolari
Ci sono 15 apeirotopi complessi regolari in formato . Coxeter esprime 12 di loro con δ p , r
4 dove q è vincolato a soddisfare q = 2 / (1 - ( p + r ) / pr ) . Questi possono anche essere decomposti come apeirotopi del prodotto: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() . Il primo caso è il favo tesserattico . Il favo a 16 celle e il favo a 24 celle sono soluzioni reali. L'ultima soluzione generata ha elementi politopo Witting .
. Il primo caso è il favo tesserattico . Il favo a 16 celle e il favo a 24 celle sono soluzioni reali. L'ultima soluzione generata ha elementi politopo Witting .
| Spazio | Gruppo | 4-apeirotopo | Vertice | Bordo | Viso | Cellula | 4 facce | van Oss apeirogon |
Appunti |
|---|---|---|---|---|---|---|---|---|---|
| p [4] 2 [3] 2 [3] 2 [4] r | δ p , r 4 = p {4} 2 {3} 2 {3} 2 {4} r |
p {} | p {4} 2 | p {4} 2 {3} 2 | p {4} 2 {3} 2 {3} 2 | p { q } r | Uguale a |
||
| 2 [4] 2 [3] 2 [3] 2 [4] 2 | δ 2,2 4 = {4,3,3,3} |
{} | {4} | {4,3} | {4,3,3} | {∞} |
Favo tesserattico Uguale a |
||
|
2 [3] 2 [4] 2 [3] 2 [3] 2 = [3,4,3,3] |
{3,3,4,3} |
1 | 12 {} | 32 {3} | 24 {3,3} | 3 {3,3,4} | Nido d'ape reale a 16 celle Uguale a |
||
| {3,4,3,3} |
3 | 24 {} | 32 {3} | 12 {3,4} | 1 {3,4,3} | Vero nido d'ape a 24 celle Uguale a |
|||
| 3 [3] 3 [3] 3 [3] 3 [3] 3 |
3 {3} 3 {3} 3 {3} 3 {3} 3 |
1 | 80 3 {} | 270 3 {3} 3 | 80 3 {3} 3 {3} 3 | 1 3 {3} 3 {3} 3 {3} 3 | 3 {4} 6 | rappresentanza 5 21 |
5-apeirotopi complessi regolari e superiori
Ci sono solo 12 apeirotopi complessi regolari in o superiori, espressi δ p , r
n dove q è vincolato a soddisfare q = 2 / (1 - ( p + r ) / pr ) . Questi possono anche essere decomposti come un prodotto di n apeirogons: ![]()
![]()
![]()
![]()
![]() ...
... ![]()
![]()
![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
![]()
![]()
![]() ...
... ![]()
![]()
![]()
![]()
![]()
![]()
![]() . Il primo caso è il vero favo dell'ipercubo .
. Il primo caso è il vero favo dell'ipercubo .
| Spazio | Gruppo | 5-apeirotopi | Vertici | Bordo | Viso | Cellula | 4 facce | 5 facce | van Oss apeirogon |
Appunti |
|---|---|---|---|---|---|---|---|---|---|---|
| p [4] 2 [3] 2 [3] 2 [3] 2 [4] r | δ p , r 5 = p {4} 2 {3} 2 {3} 2 {3} 2 {4} r |
p {} | p {4} 2 | p {4} 2 {3} 2 | p {4} 2 {3} 2 {3} 2 | p {4} 2 {3} 2 {3} 2 {3} 2 | p { q } r | Uguale a |
||
|
2 [4] 2 [3] 2 [3] 2 [3] 2 [4] 2 = [4,3,3,3,4] |
δ 2,2 5 = {4,3,3,3,4} |
{} | {4} | {4,3} | {4,3,3} | {4,3,3,3} | {∞} |
Nido d'ape da 5 cubi Uguale a |
poligono di van Oss
Un poligono di van Oss è un poligono regolare nel piano (piano reale o piano unitario ) in cui si trovano sia un bordo che il baricentro di un politopo regolare e formato da elementi del politopo. Non tutti i politopi regolari hanno poligoni di Van Oss.
Ad esempio, i poligoni di van Oss di un vero ottaedro sono i tre quadrati i cui piani passano per il suo centro. Al contrario, un cubo non ha un poligono di van Oss perché il piano da bordo a centro taglia diagonalmente due facce quadrate ei due bordi del cubo che giacciono nel piano non formano un poligono.
I favi infiniti hanno anche apeirogons di Van Oss . Ad esempio, la piastrellatura quadrata reale e la piastrellatura triangolare hanno apeirogons {∞} van Oss apeirogons.
Se esiste, il poligono di van Oss del politopo complesso regolare della forma p { q } r { s } t ... ha p- bordi.
Polytopes complessi non regolari
Polytopes complessi del prodotto
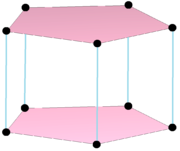 Poligono prodotto complesso |
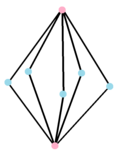 Il doppio poligono, {} + 5 {} ha 7 vertici centrati sui bordi dell'originale, collegati da 10 bordi. La sua rappresentazione reale è una bipiramide pentagonale . |
Alcuni politopi complessi possono essere rappresentati come prodotti cartesiani . Questi politopi prodotti non sono strettamente regolari poiché avranno più di un tipo di sfaccettatura, ma alcuni possono rappresentare una simmetria inferiore di forme regolari se tutti i politopi ortogonali sono identici. Ad esempio, il prodotto p {} × p {} o ![]()
![]()
![]() di due politopi unidimensionali è uguale al normale p {4} 2 o
di due politopi unidimensionali è uguale al normale p {4} 2 o ![]()
![]()
![]() . Prodotti più generali, come p {} × q {} hanno rappresentazioni reali come i duoprismi 4-dimensionali p - q . Il duale di un politopo del prodotto può essere scritto come una somma p {} + q {} e avere rappresentazioni reali come la duopiramide p - q a 4 dimensioni . Il p {} + p {} può avere la sua simmetria raddoppiata come un politopo complesso regolare 2 {4} p o
. Prodotti più generali, come p {} × q {} hanno rappresentazioni reali come i duoprismi 4-dimensionali p - q . Il duale di un politopo del prodotto può essere scritto come una somma p {} + q {} e avere rappresentazioni reali come la duopiramide p - q a 4 dimensioni . Il p {} + p {} può avere la sua simmetria raddoppiata come un politopo complesso regolare 2 {4} p o ![]()
![]()
![]() .
.
Allo stesso modo, un poliedro complesso può essere costruito come un triplo prodotto: p {} × p {} × p {} o ![]()
![]()
![]()
![]()
![]() è lo stesso del cubo generalizzato regolare , p {4} 2 {3} 2 o
è lo stesso del cubo generalizzato regolare , p {4} 2 {3} 2 o ![]()
![]()
![]()
![]()
![]() , così come il prodotto p {4} 2 × p {} o
, così come il prodotto p {4} 2 × p {} o ![]()
![]()
![]()
![]()
![]() .
.
Poligoni quasiregolari
Un poligono quasiregolare è un troncamento di un poligono regolare. Un poligono quasiregolare ![]()
![]()
![]() contiene bordi alternativi dei poligoni regolari
contiene bordi alternativi dei poligoni regolari ![]()
![]()
![]() e
e ![]()
![]()
![]() . Il poligono quasiregolare ha p vertici sugli archi p della forma regolare.
. Il poligono quasiregolare ha p vertici sugli archi p della forma regolare.
Apeirogons quasiregolari
Ci sono 7 apeirogon complessi quasiregolari che alternano i bordi di un apeirogon regolare e del suo duale regolare. Le disposizioni dei vertici di questi apeirogon hanno rappresentazioni reali con le tassellature regolari e uniformi del piano euclideo. L'ultima colonna per il 6 {3} 6 apeirogon non è solo auto-duale, ma il duale coincide con se stesso con bordi esagonali sovrapposti, quindi la loro forma quasiregolare ha anche bordi esagonali sovrapposti, quindi non può essere disegnata con due colori alternati come gli altri. La simmetria delle famiglie auto-duali può essere raddoppiata, creando così una geometria identica alle forme regolari: ![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
| p [ q ] r | 4 [8] 2 | 4 [4] 4 | 6 [6] 2 | 6 [4] 3 | 3 [12] 2 | 3 [6] 3 | 6 [3] 6 |
|---|---|---|---|---|---|---|---|
| Regolare |
 |
 |
 |
 |
 |
 |
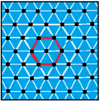 |
| Quasiregular |
 |
 |
 |
 |
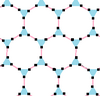 |
 |
 |
| Doppio regolare |
 |
 |
 |
 |
 |
 |
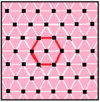 |
Poliedri quasiregolari
Come i veri politopi, un poliedro quasiregolare complesso può essere costruito come una rettifica (un troncamento completo ) di un poliedro regolare. I vertici vengono creati a metà del bordo del poliedro regolare e le facce del poliedro regolare e il suo duale sono posizionati alternativamente sui bordi comuni.
Ad esempio, un cubo p-generalizzato, ![]()
![]()
![]()
![]()
![]() , ha p 3 vertici, 3 p 2 bordi e 3 p p- facce quadrate generalizzate, mentre l' ottaedro p -generalizzato,
, ha p 3 vertici, 3 p 2 bordi e 3 p p- facce quadrate generalizzate, mentre l' ottaedro p -generalizzato, ![]()
![]()
![]()
![]()
![]() , ha 3 p vertici, 3 p 2 bordi ep 3 facce triangolari. La forma quasiregolare centrale p -cubottaedro generalizzato ,
, ha 3 p vertici, 3 p 2 bordi ep 3 facce triangolari. La forma quasiregolare centrale p -cubottaedro generalizzato , ![]()
![]()
![]()
![]()
![]() , ha 3 p 2 vertici, 3 p 3 bordi e 3 p + p 3 facce.
, ha 3 p 2 vertici, 3 p 3 bordi e 3 p + p 3 facce.
Anche la rettifica del poliedro dell'Assia ![]()
![]()
![]()
![]()
![]() , è
, è ![]()
![]()
![]()
![]()
![]() , una forma quasiregolare che condivide la geometria del poliedro complesso regolare
, una forma quasiregolare che condivide la geometria del poliedro complesso regolare ![]()
![]()
![]()
![]()
![]() .
.
| Cubo / ottaedri generalizzati | Poliedro dell'Assia | |||||
|---|---|---|---|---|---|---|
| p = 2 (reale) | p = 3 | p = 4 | p = 5 | p = 6 | ||
Cubi generalizzati (regolare) |
 Cubo |
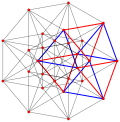 |
 |
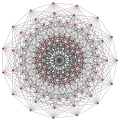 |
 |
 |
Cubottaedra generalizzato (quasiregolare) |
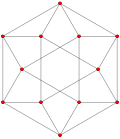 Cubottaedro |
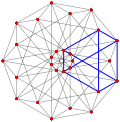 |
 |
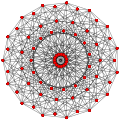 |
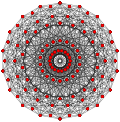 |
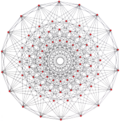 |
Ottaedri generalizzati (regolare) |
 Ottaedro |
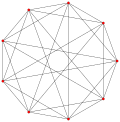 |
 |
 |
 |
 |
Altri politopi complessi con riflessioni unitarie del periodo due
Altri politopi complessi non regolari possono essere costruiti all'interno di gruppi di riflessione unitari che non realizzano grafici di Coxeter lineari. Nei diagrammi di Coxeter con loop Coxeter segna un interno del periodo speciale, come ![]()
![]()
![]() o il simbolo (1 1 1 1) 3 e il gruppo [1 1 1] 3 . Questi politopi complessi non sono stati esplorati sistematicamente al di là di pochi casi.
o il simbolo (1 1 1 1) 3 e il gruppo [1 1 1] 3 . Questi politopi complessi non sono stati esplorati sistematicamente al di là di pochi casi.
Il gruppo ![]()
![]()
![]() è definito da 3 riflessioni unitarie, R 1 , R 2 , R 3 , tutti di ordine 2: R 1 2 = R 1 2 = R 3 2 = (R 1 R 2 ) 3 = (R 2 R 3 ) 3 = (R 3 R 1 ) 3 = (R 1 R 2 R 3 R 1 ) p = 1. Il periodo p può essere visto come una doppia rotazione in reale .
è definito da 3 riflessioni unitarie, R 1 , R 2 , R 3 , tutti di ordine 2: R 1 2 = R 1 2 = R 3 2 = (R 1 R 2 ) 3 = (R 2 R 3 ) 3 = (R 3 R 1 ) 3 = (R 1 R 2 R 3 R 1 ) p = 1. Il periodo p può essere visto come una doppia rotazione in reale .
Come con tutte le costruzioni di Wythoff , politopi generati da riflessioni, il numero di vertici di un politopo del diagramma di Coxeter ad anello singolo è uguale all'ordine del gruppo diviso per l'ordine del sottogruppo in cui viene rimosso il nodo ad anello. Ad esempio, un vero cubo ha il diagramma di Coxeter ![]()
![]()
![]()
![]()
![]() , con simmetria ottaedrica
, con simmetria ottaedrica ![]()
![]()
![]()
![]()
![]() ordine 48 e simmetria diedro del sottogruppo
ordine 48 e simmetria diedro del sottogruppo ![]()
![]()
![]() ordine 6, quindi il numero di vertici di un cubo è 48/6 = 8. Le sfaccettature vengono costruite rimuovendo un nodo più lontano dal nodo inanellato, ad esempio
ordine 6, quindi il numero di vertici di un cubo è 48/6 = 8. Le sfaccettature vengono costruite rimuovendo un nodo più lontano dal nodo inanellato, ad esempio ![]()
![]()
![]() per il cubo. Le figure dei vertici vengono generate rimuovendo un nodo inanellato e facendo squillare uno o più nodi connessi, e
per il cubo. Le figure dei vertici vengono generate rimuovendo un nodo inanellato e facendo squillare uno o più nodi connessi, e ![]()
![]()
![]() per il cubo.
per il cubo.
Coxeter rappresenta questi gruppi con i seguenti simboli. Alcuni gruppi hanno lo stesso ordine, ma una struttura diversa, definendo la stessa disposizione dei vertici in politopi complessi, ma bordi diversi ed elementi superiori, come ![]()
![]()
![]() e
e ![]()
![]()
![]()
![]() con p ≠ 3.
con p ≠ 3.
| Diagramma di Coxeter | Ordine | Simbolo o posizione nella tabella VII di Shephard e Todd (1954) |
|---|---|---|
|
|
p n - 1 n !, p ≥ 3 | G ( p , p , n ), [ p ], [1 1 1] p , [1 1 ( n −2) p ] 3 |
|
|
72 · 6 !, 108 · 9! | N. 33, 34, [1 2 2] 3 , [1 2 3] 3 |
|
|
14 · 4 !, 3 · 6 !, 64 · 5! | Nn. 24, 27, 29 |
Coxeter chiama alcuni di questi poliedri complessi quasi regolari perché hanno sfaccettature regolari e figure dei vertici. La prima è una forma di simmetria inferiore del politopo incrociato generalizzato in . Il secondo è un cubo generalizzato frazionario, che riduce i p- bordi in singoli vertici lasciando 2 bordi ordinari. Tre di loro sono legati al poliedro obliquo regolare finito in .
| Spazio | Gruppo | Ordine | Simboli di Coxeter |
Vertici | Bordi | Facce | Figura del vertice |
Appunti |
|---|---|---|---|---|---|---|---|---|
| [1 1 1 p ] 3 p = 2,3,4 ... |
6 p 2 | (1 1 1 1 p ) 3 |
3 p | 3 p 2 | {3} | {2 p } | Simbolo di Shephard (1 1; 1 1 ) p uguale a β p 3 = |
|
| (1 1 1 1 p ) 3 |
p 2 | {3} | {6} | Simbolo di Shephard (1 1 1; 1) p 1 / p γ p 3 |
||||
| [1 1 1 2 ] 3 |
24 | (1 1 1 1 2 ) 3 |
6 | 12 | 8 {3} | {4} | Uguale a β 2 3 = |
|
| (1 1 1 1 2 ) 3 |
4 | 6 | 4 {3} | {3} | 1/2 γ 2 3 = |
|||
| [1 1 1] 3 |
54 | (1 1 1 1 ) 3 |
9 | 27 | {3} | {6} | Simbolo di Shephard (1 1; 1 1 ) 3 uguale a β 3 3 = |
|
| (1 1 1 1) 3 |
9 | 27 | {3} | {6} | Simbolo di Shephard (1 1 1; 1) 3 1/3 γ 3 3 = β 3 3 |
|||
| [1 1 1 4 ] 3 |
96 | (1 1 1 1 4 ) 3 |
12 | 48 | {3} | {8} | Simbolo di Shephard (1 1; 1 1 ) 4 uguale a β 4 3 = |
|
| (1 1 1 1 4 ) 3 |
16 | {3} | {6} | Simbolo di Shephard (1 1 1; 1) 4 1/4 γ 4 3 |
||||
| [1 1 1 5 ] 3 |
150 | (1 1 1 1 5 ) 3 |
15 | 75 | {3} | {10} | Simbolo di Shephard (1 1; 1 1 ) 5 uguale a β 5 3 = |
|
| (1 1 1 1 5 ) 3 |
25 | {3} | {6} | Simbolo di Shephard (1 1 1; 1) 5 1/5 γ 5 3 |
||||
| [1 1 1 6 ] 3 |
216 | (1 1 1 1 6 ) 3 |
18 | 216 | {3} | {12} | Simbolo Shephard (1 1; 1 1 ) 6 uguale a β 6 3 = |
|
| (1 1 1 1 6 ) 3 |
36 | {3} | {6} | Simbolo di Shephard (1 1 1; 1) 6 1/6 γ 6 3 |
||||
| [1 1 1 4 ] 4 |
336 | (1 1 1 1 4 ) 4 |
42 | 168 | 112 {3} | {8} | rappresentazione {3,8 |, 4} = {3,8} 8 | |
| (1 1 1 1 4 ) 4 |
56 | {3} | {6} | |||||
| [1 1 1 5 ] 4 |
2160 | (1 1 1 1 5 ) 4 |
216 | 1080 | 720 {3} | {10} | rappresentazione {3,10 |, 4} = {3,10} 8 | |
| (1 1 1 1 5 ) 4 |
360 | {3} | {6} | |||||
| [1 1 1 4 ] 5 |
(1 1 1 1 4 ) 5 |
270 | 1080 | 720 {3} | {8} | rappresentazione {3,8 |, 5} = {3,8} 10 | ||
| (1 1 1 1 4 ) 5 |
360 | {3} | {6} |
Coxeter definisce altri gruppi con costruzioni anti-unitarie, ad esempio questi tre. Il primo è stato scoperto e disegnato da Peter McMullen nel 1966.
| Spazio | Gruppo | Ordine | Simboli di Coxeter |
Vertici | Bordi | Facce | Figura del vertice |
Appunti |
|---|---|---|---|---|---|---|---|---|
| [1 1 4 1 4 ] (3) |
336 | (1 1 1 4 1 4 ) (3) |
56 | 168 | 84 {4} | {6} | rappresentazione {4,6 |, 3} = {4,6} 6 | |
| [1 5 1 4 1 4 ] (3) |
2160 | (1 1 5 1 4 1 4 ) (3) |
216 | 1080 | 540 {4} | {10} | rappresentazione {4,10 |, 3} = {4,10} 6 | |
| [1 4 1 5 1 5 ] (3) |
(1 1 4 1 5 1 5 ) (3) |
270 | 1080 | 432 {5} | {8} | rappresentazione {5,8 |, 3} = {5,8} 6 |
| Spazio | Gruppo | Ordine | Simboli di Coxeter |
Vertici | Altri elementi |
Cellule | Figura del vertice |
Appunti |
|---|---|---|---|---|---|---|---|---|
| [1 1 2 p ] 3 p = 2,3,4 ... |
24 p 3 | (1 1 2 2 p ) 3 |
4 p | Shephard (2 2 1; 1) p uguale a β p 4 = |
||||
| (1 1 1 2 p ) 3 |
p 3 |
|
Shephard (2 1; 1 1 ) p 1 / p γ p 4 |
|||||
| [1 1 2 2 ] 3 = [3 1,1,1 ] |
192 | (1 1 2 2 2 ) 3 |
8 | 24 bordi 32 facce |
16 |
β 2 4 = |
||
| (1 1 1 2 2 ) 3 |
1/2 γ 2 4 = 4 , 16 celle reali |
|||||||
| [1 1 2] 3 |
648 | (1 1 2 2 ) 3 |
12 | Shephard (2 2 1; 1) 3 uguale a β 3 4 = |
||||
| (1 1 1 2 3 ) 3 |
27 |
|
Shephard (2 1; 1 1 ) 3 1/3 γ 3 4 |
|||||
| [1 1 2 4 ] 3 |
1536 | (1 1 2 2 4 ) 3 |
16 | Shephard (2 2 1; 1) 4 uguale a β 4 4 = |
||||
| (1 1 1 2 4 ) 3 |
64 |
|
Shephard (2 1; 1 1 ) 4 1/4 γ 4 4 |
|||||
| [1 4 1 2] 3 |
7680 | (2 2 1 4 1) 3 |
80 | Shephard (2 2 1; 1) 4 | ||||
| (1 1 4 1 2) 3 |
160 |
|
Shephard (2 1; 1 1 ) 4 | |||||
| (1 1 1 4 2) 3 |
320 |
|
Shephard (2 1 1 ; 1) 4 | |||||
| [1 1 2] 4 |
(1 1 2 2 ) 4 |
80 | 640 bordi 1280 triangoli |
640 |
||||
| (1 1 1 2) 4 |
320 |
|
| Spazio | Gruppo | Ordine | Simboli di Coxeter |
Vertici | Bordi | Sfaccettature | Figura del vertice |
Appunti |
|---|---|---|---|---|---|---|---|---|
| [1 1 3 p ] 3 p = 2,3,4 ... |
120 p 4 | (1 1 3 3 p ) 3 |
5 p | Shephard (3 3 1; 1) p uguale a β p 5 = |
||||
| (1 1 1 3 p ) 3 |
p 4 |
|
Shephard (3 1; 1 1 ) p 1 / p γ p 5 |
|||||
| [2 2 1] 3 |
51840 | (2 1 2 2 ) 3 |
80 |
|
Shephard (2 1; 2 2 ) 3 | |||
| (2 1 1 2) 3 |
432 | Shephard (2 1 1 ; 2) 3 |
| Spazio | Gruppo | Ordine | Simboli di Coxeter |
Vertici | Bordi | Sfaccettature | Figura del vertice |
Appunti |
|---|---|---|---|---|---|---|---|---|
| [1 1 4 p ] 3 p = 2,3,4 ... |
720 p 5 | (1 1 4 4 p ) 3 |
6 p | Shephard (4 4 1; 1) p uguale a β p 6 = |
||||
| (1 1 1 4 p ) 3 |
p 5 |
|
Shephard (4 1; 1 1 ) p 1 / p γ p 6 |
|||||
| [1 2 3] 3 |
39191040 | (2 1 3 3 ) 3 |
756 |
|
Shephard (2 1; 3 3 ) 3 | |||
| (2 2 1 3) 3 |
4032 |
|
Shephard (2 2 1; 3) 3 | |||||
| (2 1 1 3) 3 |
54432 |
|
Shephard (2 1 1 ; 3) 3 |
Visualizzazioni
Guarda anche
Appunti
Riferimenti
- Coxeter, HSM e Moser, WOJ; Generatori e relazioni per gruppi discreti (1965), in particolare pp 67-80.
- Coxeter, HSM (1991), Regular Complex Polytopes , Cambridge University Press, ISBN 0-521-39490-2 Manutenzione CS1: parametro sconsigliato ( collegamento )
- Coxeter, HSM e Shephard, GC; Ritratti di una famiglia di politopi complessi, Leonardo Vol 25, No 3/4, (1992), pp 239–244,
- Shephard, GC; Polytopes complessi regolari , Proc. Matematica di Londra. Soc. Serie 3, Vol 2, (1952), pagg. 82–97.
- GC Shephard , JA Todd, gruppi di riflessione unitari finiti , Canadian Journal of Mathematics. 6 (1954), 274-304 [2]
- Gustav I. Lehrer e Donald E. Taylor, Unitary Reflection Groups , Cambridge University Press 2009
Ulteriore lettura
- F. Arthur Sherk, Peter McMullen, Anthony C. Thompson e Asia Ivić Weiss, editori: Kaleidoscopes - Selected Writings of HSM Coxeter. , Documento 25, Gruppi finiti generati da riflessioni unitarie , p 415-425, John Wiley, 1995, ISBN 0-471-01003-0
- McMullen, Peter ; Schulte, Egon (dicembre 2002), Abstract Regular Polytopes (1a ed.), Cambridge University Press , ISBN 0-521-81496-0 Capitolo 9 Gruppi unitari e forme hermitiane , pp. 289–298










![{\ displaystyle \ left [{\ begin {smallmatrix} e ^ {2 \ pi i / p} & 0 \\ (e ^ {2 \ pi i / p} -1) k & 1 \\\ end {smallmatrix}} \ right ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d128407ddca614c4bed7308acba9bd274b704c5c)
![{\ displaystyle \ left [{\ begin {smallmatrix} 1 & (e ^ {2 \ pi i / r} -1) k \\ 0 & e ^ {2 \ pi i / r} \\\ end {smallmatrix}} \ right ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de7bd24e7be60162da1fa1566fea5571820d3e82)

![{\ displaystyle \ left [{\ begin {smallmatrix} e ^ {2 \ pi i / p} & 0 \\ 0 & 1 \\\ end {smallmatrix}} \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/922057855ba2380fdbf36b0e91f0afe08b867bcb)
![{\ displaystyle \ left [{\ begin {smallmatrix} 1 & 0 \\ 0 & e ^ {2 \ pi i / q} \\\ end {smallmatrix}} \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6991a4012a94e23b3475fd268007ca2aeba4bcbe)
![{\ displaystyle \ left [{\ begin {smallmatrix} 0 & 1 \\ 1 & 0 \\\ end {smallmatrix}} \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9694a3311550c844e792232f8c8742c6f3c9d32f)
![{\ displaystyle \ left [{\ begin {smallmatrix} {\ frac {-1 + {\ sqrt {3}} i} {2}} & 0 \\ {\ frac {-3 + {\ sqrt {3}} i } {2}} & 1 \\\ end {smallmatrix}} \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aef7975113174eb40a8488733bebb8fb4d1bd293)
![{\ displaystyle \ left [{\ begin {smallmatrix} 1 & {\ frac {-3 + {\ sqrt {3}} i} {2}} \\ 0 & {\ frac {-1 + {\ sqrt {3}} i} {2}} \\\ end {smallmatrix}} \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1081ee946ee626dd6ae6d776581d567006cd16fb)
![{\ displaystyle \ left [{\ begin {smallmatrix} i & 0 \\ 0 & 1 \\\ end {smallmatrix}} \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4087d1ec8773364a46947bc9f58bf721a413846c)
![{\ displaystyle \ left [{\ begin {smallmatrix} 1 & 0 \\ 0 & i \\\ end {smallmatrix}} \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3736413b59866ae2edd640f7bb77f7b8bdd6a9d)
![{\ displaystyle \ left [{\ begin {smallmatrix} 1 & -2 \\ 0 & -1 \\\ end {smallmatrix}} \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de49a4aea18b37177252a0f6c2a3707c14b9b910)